题目内容
17.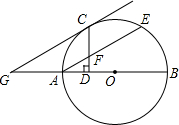 如图,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于D,过C作CG∥AE交BA的延长线于点G.
如图,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于D,过C作CG∥AE交BA的延长线于点G.(1)求证:CG是⊙O的切线;
(2)若∠EAB=30°,CF=2,求AG的长.
分析 (1)连接OC,欲证明CG是⊙O的切线,只要证明OC⊥CG即可.
(2)连接AC,先证明△AOC是等边三角形,求出AF、DF、AD,再根据CG∥AE得$\frac{DF}{CF}$=$\frac{AD}{AG}$,由此即可计算.
解答 (1)证明:连接OC.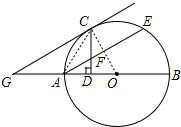 ∵AE是弦,C是劣弧AE的中点,
∵AE是弦,C是劣弧AE的中点,
∴OC⊥AE.,
∵CG∥AE,
∴OC⊥GC,
∴CG是⊙O的切线.
(2)解:连接AC.
∵∠EAB=30°,CG∥AE,
∴∠G=∠EAB=30°,
∵CG是⊙O的切线,
∴∠GCO=90°,
∴∠COA=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠CAO=60°,
∴∠CAF=30°,
可求∠ACD=30°,
∴AF=CF=2,
∵∠EAB=30°,
∴DF=1,AD=$\sqrt{3}$,
∵CG∥AE,
∴$\frac{DF}{CF}$=$\frac{AD}{AG}$,
∴$\frac{1}{2}$=$\frac{\sqrt{3}}{AG}$,
∴AG=2$\sqrt{3}$.
点评 本题考查切线的判定和性质、平行线的性质、等边三角形的判定和性质、直角三角形30度角性质、垂径定理等知识,解题的关键是掌握切线的判定方法,灵活运用圆的有关知识,属于中考常考题型.

练习册系列答案
相关题目
8.若x1,x2是一元二次方程x2+ax-8=0的两个根,则x1•x2的值是( )
| A. | a | B. | -a | C. | 8 | D. | -8 |
5.下列事件中最适合使用普查方式收集数据的是( )
| A. | 了解某班同学的体重情况 | B. | 了解我省初中学生的兴趣爱好情况 | ||
| C. | 了解一批电灯泡的使用寿命 | D. | 了解我省农民工的年收入情况 |
12.一枚质地均匀的六面骰子,六个面上分别刻有1,2,3,4,5,6点,投掷一次得到的点数为奇数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2. 某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
 某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )| A. | 7,7 | B. | 8,7.5 | C. | 7,8 | D. | 8,7 |
6.抛物线y=x2+2x-1,与x轴的交点个数是( )
| A. | 1个交点 | B. | 2个交点 | C. | 1个或2个交点 | D. | 没有交点 |
7.若正多边形的一个内角是120°,则这个正多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
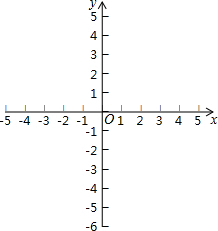 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点(0,-3),(2,-3).