题目内容
19.先化简,再求值:$(\frac{x^2}{x-1}-x+1)÷\frac{{4{x^2}-4x+1}}{1-x}$,其中x满足x2+2x-3=0.分析 先算括号里面的,再算除法,根据x满足x2+2x-3=0求出x的值,代入分式进行计算即可.
解答 解:原式=$\frac{{x}^{2}-{(x-1)}^{2}}{x-1}$•$\frac{1-x}{{(2x-1)}^{2}}$
=$\frac{2x-1}{x-1}$•$\frac{1-x}{{(2x-1)}^{2}}$
=$-\frac{1}{2x-1}$,
由x2+2x-3=0解得,x1=-3,x2=1,
∵x≠1,
∴当x=-3时,原式=-$\frac{1}{2×(-3)-1}$=$\frac{1}{7}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
7.若正多边形的一个内角是120°,则这个正多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
14.下列几何图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 菱形 | D. | 正五边形 |
8.五张标有2、2、3、4、5的卡片,除数字外,其他没有任何区别,现将它们背面朝上,从中任取一张,得到卡片的数字为偶数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
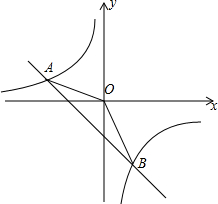 如图,一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、
如图,一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、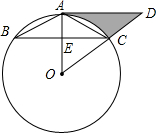 如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.
如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.