题目内容
12. 在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.
在?ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF.(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
分析 (1)由平行四边形的性质和已知条件得出BE=DF,证明四边形BFDE为平行四边形,再由DE⊥AB,即可得出结论;
(2)由矩形的性质和勾股定理求出BC,得出AD=BC=DF,证出∠DAF=∠DFA,再由平行线的性质即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CF=AE,
∴BE=DF.
∴四边形BFDE为平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
(2)证明:由(1)得,四边形BFDE是矩形,
∴∠BFD=90°.
∴∠BFC=90°,
在Rt△BFC中,由勾股定理得:BC=$\sqrt{C{F}^{2}+B{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
∴AD=BC=10.
∵DF=10,
∴AD=DF.
∴∠DAF=∠DFA.
∵AB∥CD,
∴∠DFA=∠FAB.
∴∠DAF=∠FAB.
∴AF平分∠DAB.
即AF是∠DAB的平分线.
点评 本题考查了平行四边形的性质、矩形的判定与性质、勾股定理、等腰三角形的判定;熟练掌握平行四边形的性质,证明四边形BFDE是矩形是解决问题的关键.

练习册系列答案
相关题目
2. 某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
 某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )| A. | 7,7 | B. | 8,7.5 | C. | 7,8 | D. | 8,7 |
7.若正多边形的一个内角是120°,则这个正多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
17.射线AD、AE分别与⊙O相切于D、E两点,直线BC与⊙O相切于点F,分别交AD、AE于点B、C,若∠A=40°.则∠BOC等于( )
| A. | 70° | B. | 110° | C. | 70°或110° | D. | 40°或140° |
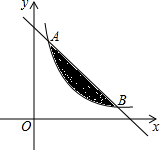 平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点.如图,直线y=-x+7和反比例函数y=$\frac{6}{x}$(x>0)的图象交于A,B两点,则落在图中阴影部分(不包含边界)内的整点个数有( )个.
平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点.如图,直线y=-x+7和反比例函数y=$\frac{6}{x}$(x>0)的图象交于A,B两点,则落在图中阴影部分(不包含边界)内的整点个数有( )个.