题目内容
2．
如图所示的图象是抛物线y=ax2+2ax+a2+2的一部分，它与x轴的一个交点A的坐标是（-3，0），则它与x轴的另一个交点的坐标为（1，0）．
分析 根据图象可知抛物线y=ax2+2ax+a2+2的对称轴为x=-1，可求得抛物线和x轴的另一个交点坐标．
解答 解：∵抛物线y=ax2+2ax+a2+2的对称轴为x=-$\frac{2a}{2a}$=-1，
∴该抛物线与x轴的另一个交点到x=-1的距离为2，
∵它与x轴的一个交点A的坐标是（-3，0），
∴抛物线y=ax2+2ax+a2+2与x轴的另一个交点坐标为（1，0）．
故答案为：（1，0）．
点评 本题考查了抛物线和x轴的交点问题，注：抛物线与x轴的交点问题的两个交点到对称轴的距离相等．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
12．一枚质地均匀的六面骰子，六个面上分别刻有1，2，3，4，5，6点，投掷一次得到的点数为奇数的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
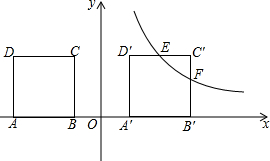如图，在平面直角坐标系中，正方形ABCD顶点D（-3，2），B（1，0），CD∥x轴，将正方形ABCD向右平移m个单位，得正方形A′B′C′D′．当 m=4时，反比例函数y=$\frac{k}{x}$（x＞0）的图象过线段C′D′的中点E，与线段B′C′交于点F．
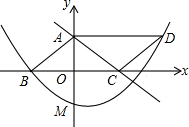如图，平行四边形ABCD中，D点在抛物线y=$\frac{1}{8}$x2+bx+c上，且OB=OC，AB=5，tan∠ACB=$\frac{3}{4}$，M是抛物线与y轴的交点．
7．若正多边形的一个内角是120°，则这个正多边形的边数为（ ）
| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
14．下列几何图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． | 等腰三角形 | B． | 等边三角形 | C． | 菱形 | D． | 正五边形 |
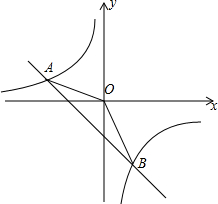如图，一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、