题目内容
19.某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线.(1)请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法);
(2)求小明到达点F时的影长FH的长.
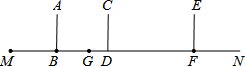
分析 (1)连结MA、GC并延长MA和GC,它们相交于点O,然后连结OE并延长交MN于H,则FH为小明位于点F时在这个灯光下的影长;
(2)先利用速度公式得到BM=BD=3m,DF=4.5m,设AB=CD=EF=a,作OK⊥MN于K,如图,通过证明△MAB∽△MOK得到$\frac{a}{OK}$=$\frac{3}{6+DK}$①,通过证明△GCD∽△GOK得到$\frac{a}{OK}$=$\frac{1.2}{1.2+DK}$②,由①②得$\frac{3}{6+DK}$=$\frac{1.2}{1.2+DK}$,可求出Dk=2,原式得到$\frac{a}{OK}$=$\frac{3}{8}$,FK=DF-DK=2.5,然后证明△HEF∽△HOK,利用相似比可计算出HF.
解答 解:(1)如图,点O和FH为所作;
(2)BM=BD=2×1.5=3m,GD=1.2m,DF=1.5×1.5×2=4.5m,设AB=CD=EF=a,
作OK⊥MN于K,如图,
∵AB∥OK,
∴△MAB∽△MOK,
∴$\frac{AB}{OK}$=$\frac{MB}{MK}$,即$\frac{a}{OK}$=$\frac{3}{6+DK}$①,
∵CD∥OK,
∴△GCD∽△GOK,
∴$\frac{CD}{OK}$=$\frac{GD}{GK}$,即$\frac{a}{OK}$=$\frac{1.2}{1.2+DK}$②,
由①②得$\frac{3}{6+DK}$=$\frac{1.2}{1.2+DK}$,解得Dk=2,
∴$\frac{a}{OK}$=$\frac{3}{6+2}$=$\frac{3}{8}$,FK=DF-DK=4.5-2=2.5,
∵EF∥OK,
∴△HEF∽△HOK,
∴$\frac{a}{OK}$=$\frac{HF}{HK}$,即$\frac{HF}{HF+2.5}$=$\frac{3}{8}$,
∴HF=1.5(m).
答:小明到达点F时的影长FH的长为1.5m.
点评 本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.也考查了构建相似三角形,利用相似三角形的性质计算相应线段的长.

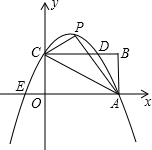 如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )| A. | $\frac{7}{4}$$\sqrt{3}$ | B. | $\frac{7}{16}$$\sqrt{3}$ | C. | $\frac{7}{8}$$\sqrt{3}$ | D. | $\frac{7}{8}$ |
| A. | (a2+1)4 | B. | (a2+1)2 | C. | a2+1 | D. | $\sqrt{{a^2}+1}$ |
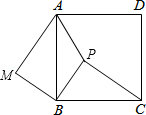 正方形ABCD内有一点P,连接AP,BP,CP,将△PBC绕点B逆时针旋转至BC与AB重合,得到△ABM.
正方形ABCD内有一点P,连接AP,BP,CP,将△PBC绕点B逆时针旋转至BC与AB重合,得到△ABM.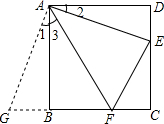 如图,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.
如图,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.