题目内容

7．化简：当m＜1时，|m-1|+|m-3|=-2m+4．

分析 先根据绝对值的性质把原式化简，再去括号即可．

解答 解：当m＜1时，
m-1＜0，m-3＜0，
则|m-1|+|m-3|=-（m-1）-（m-3）=-m+1-m+3=-2m+4．
故答案为：-2m+4．

点评 此题考查绝对值，掌握绝对值的意义与性质是解决问题的关键．

练习册系列答案
相关题目
17．如图所示，已知∠B=∠BGD，∠DGF=∠F，求证：AB∥EF．
18．如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．在图（1）中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．根据点P所在的不同位置，试探究下列问题：
在图（2），（3），（4），（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）如图②，点P在线段MC上，直接写出h1、h2、h3、h之间的关系；
（2）如图③，点P在△ABC内，写出h1、h2、h3、h之间的关系，并说明理由；
（3）如图④，点P在线段MC的延长线上，试猜想h1、h2、h3、h之间存在什么关系？（直接写结论）
（4）如图⑤，点P在△ABC外，写出h1、h2、h3、h之间的关系，并说明理由．
15．已知在直角坐标系中，半径为5的⊙P与坐标轴恰好有三个交点，求圆心P的位置，并画出相应的图形．
2．若记y=f（x）=$\frac{{x}^{2}}{1+{x}^{2}}$，其中f（1）表示当x=1时y的值，即f（1）=$\frac{{1}^{2}}{1+{1}^{1}}$；f（$\frac{1}{2}$）表示x=$\frac{1}{2}$时y的值，即f（$\frac{1}{2}$）=$\frac{（\frac{1}{2}）^{2}}{1+（\frac{1}{2}）^{2}}$=$\frac{1}{5}$，…
求f（1）+f（2）+f（$\frac{1}{2}$）+f（3）+f（$\frac{1}{3}$）+…+f（2015）+f（$\frac{1}{2015}$）=$\frac{4029}{2}$．
12．有下列式子：-$\frac{1}{2}$（a-b），-$\frac{{x}^{2}y}{2}$，2m，0.1x，$\frac{{y}^{2}+y+1}{y}$，$\frac{2x-y}{3}$，1-$\frac{1}{y}$，其中整式有5个．
19．下列选项中，与-$\frac{2}{5}$互为相反数的是（　　）
A．-$\frac{2}{5}$B．$\frac{2}{5}$C．-$\frac{5}{2}$D．$\frac{5}{2}$
16．下列不属于分式$\frac{1}{2{x}^{2}-18}$与$\frac{x}{4x+12}$的公分母的是（　　）
A．（2x2-18）（4x+12）B．16（x-3）（x+3）C．4（x-3）（x+3）D．2（x+3）（x-3）
14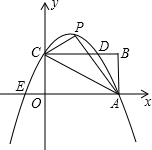．如图，矩形OABC的长OA=$\sqrt{3}$，宽OC=1，将△AOC沿AC翻折得△APC，经过C，P，A三点的抛物线与矩形OABC边CB相交于点D，则梯形COAD的面积为（　　）
A．$\frac{7}{4}$$\sqrt{3}$B．$\frac{7}{16}$$\sqrt{3}$C．$\frac{7}{8}$$\sqrt{3}$D．$\frac{7}{8}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网