题目内容
5.已知正△ABC内接于圆O,四边形DEFG为半圆O的内接正方形(D,E在直径上,F,G在半圆上的正方形),S△ABC=a,S四边形DEFG=b,则$\frac{b}{a}$的值等于$\frac{16\sqrt{3}}{45}$.分析 设圆O的半径为R,由正三角形的性质得出S△ABC=a=$\frac{3\sqrt{3}}{4}$R2,连接OF,设正方形DEFG的边长为2x,则OE=x,由勾股定理和正方形的性质得出x2=$\frac{{R}^{2}}{5}$,得出正方形DEFG的面积=$\frac{4}{5}{R}^{2}$,即b═$\frac{4}{5}{R}^{2}$,即可得出结果.
解答 解:如图所示: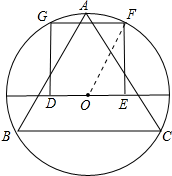 连接OF,
连接OF,
设圆O的半径为R,
∵△ABC是正三角形,
∴S△ABC=a=$\frac{3\sqrt{3}}{4}$R2,
设正方形DEFG的边长为2x,则OE=x,
∴OF2=OE2+EF2=x2+(2x)2=5x2,
即R2=5x2,
∴x2=$\frac{{R}^{2}}{5}$,
∴正方形DEFG的面积=(2x)2=4x2=$\frac{4}{5}{R}^{2}$,
即b═$\frac{4}{5}{R}^{2}$,
∴$\frac{b}{a}$=$\frac{\frac{4}{5}{R}^{2}}{\frac{3\sqrt{3}}{4}{R}^{2}}$=$\frac{16\sqrt{3}}{45}$.
点评 本题考查了正三角形的性质、正方形的性质、正多边形和圆的关系、勾股定理等知识;本题综合性强,有一定难度,把正三角形和正方形的面积用半径R表示出来是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列选项中,与-$\frac{2}{5}$互为相反数的是( )
| A. | -$\frac{2}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{5}{2}$ | D. | $\frac{5}{2}$ |
16.下列不属于分式$\frac{1}{2{x}^{2}-18}$与$\frac{x}{4x+12}$的公分母的是( )
| A. | (2x2-18)(4x+12) | B. | 16(x-3)(x+3) | C. | 4(x-3)(x+3) | D. | 2(x+3)(x-3) |
14.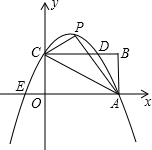 如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
 如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )| A. | $\frac{7}{4}$$\sqrt{3}$ | B. | $\frac{7}{16}$$\sqrt{3}$ | C. | $\frac{7}{8}$$\sqrt{3}$ | D. | $\frac{7}{8}$ |
15.下列根式是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{a}}$ | B. | $\sqrt{8a}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{{a}^{2}b}$ |

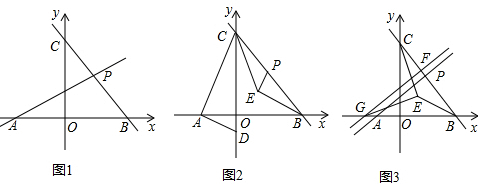
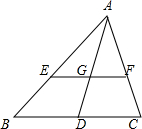 如图,在△ABC中,AD为BC边上的中线,EF∥BC,分别交AC于点E,F,交AD于点G,求证:EG=GF.
如图,在△ABC中,AD为BC边上的中线,EF∥BC,分别交AC于点E,F,交AD于点G,求证:EG=GF.