题目内容
4．$\sqrt{8}$+$\sqrt{2}$=3$\sqrt{2}$．分析 先进行二次根式的化简，然后合并．
解答 解：$\sqrt{8}+\sqrt{2}$=2$\sqrt{2}$+$\sqrt{2}$
=3$\sqrt{2}$．
故答案为：3$\sqrt{2}$．
点评 本题考查了二次根式的加减法，解答本题的关键是掌握二次根式的化简与合并．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
14．
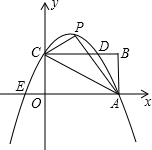如图，矩形OABC的长OA=$\sqrt{3}$，宽OC=1，将△AOC沿AC翻折得△APC，经过C，P，A三点的抛物线与矩形OABC边CB相交于点D，则梯形COAD的面积为（ ）
如图，矩形OABC的长OA=$\sqrt{3}$，宽OC=1，将△AOC沿AC翻折得△APC，经过C，P，A三点的抛物线与矩形OABC边CB相交于点D，则梯形COAD的面积为（ ）| A． | $\frac{7}{4}$$\sqrt{3}$ | B． | $\frac{7}{16}$$\sqrt{3}$ | C． | $\frac{7}{8}$$\sqrt{3}$ | D． | $\frac{7}{8}$ |
15．下列根式是最简二次根式的是（ ）
| A． | $\sqrt{\frac{1}{a}}$ | B． | $\sqrt{8a}$ | C． | $\sqrt{{a}^{2}+1}$ | D． | $\sqrt{{a}^{2}b}$ |
（1）计算：（-2）÷（-2÷$\frac{1}{2}$）-|-3|×（-1）+（-0.5）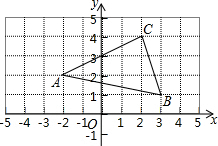
如图，边长为1的正方形网格中有格点△ABC和格点O，若把△ABC绕着点O逆时针旋转180°
9．$\sqrt{{{（{a^2}+1）}^2}}$的算术平方根是（ ）
| A． | （a2+1）4 | B． | （a2+1）2 | C． | a2+1 | D． | $\sqrt{{a^2}+1}$ |