题目内容
17.我市为了鼓励居民节约用水,对居民生活用水的收费实行阶梯式计量水价的方法,具体规定如下:| 各阶梯 | 月用水量 | 基本水价(元、立方米) |
| 第一阶梯 | 不超过28立方米的部分 | 2 |
| 第二阶梯 | 超过28立方米且不超过40立方米的部分 | 2.5 |
| 第三阶梯 | 超过40立方米的部分 | 3 |
(1)分别写出每月用水量在三个不同阶梯时,y与x的函数关系式.
(2)已知小明家4月份缴纳水费83元,则他家该月共用水多少立方米?
分析 (1)未超过28吨时,水费y=2×相应吨数;超过28立方米且不超过40立方米时,水费y=2×28+超过28吨的吨数×2.5;超过40立方米时,水费y=2×28+(40-28)×2.5+超过40立方米×3;
(2)因为小明家4月份交纳水费为83元,而56<83<86,故小明家4月份用水量在第二个阶梯,即2.5x-14=83,即可解答.
解答 解:(1)当x≤28时,y=2x;
当28<x≤40时,y=2×28+(x-28)×2.5=2.5x-14
当x>40时,y=2×28+(40-28)×2.5+(x-40)×3=3x-34.
(2)因为小明家4月份交纳水费为83元,
而56<83<86
故小明家4月份用水量在第二个阶梯,
即当y=83时,2.5x-14=83,
解得x=38.8.
答:他家该月共用水38.8立方米.
点评 本题考查一次函数的应用,解决本题的关键是得出每月用水量在三个不同阶梯时,y与x的函数关系式.

练习册系列答案
相关题目
7.化简:
(1)(a-2b)2-(2a+b)(b-2a)-4a(a-b).
(2)($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{{x}^{2}+2x+1}{{x}^{2}-4}$.
(1)(a-2b)2-(2a+b)(b-2a)-4a(a-b).
(2)($\frac{x}{{x}^{2}+2x}$-1)÷$\frac{{x}^{2}+2x+1}{{x}^{2}-4}$.
8.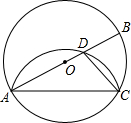 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
 在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )
在⊙O中,AB为直径,点C为圆上一点,将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数( )| A. | 35° | B. | 40° | C. | 45° | D. | 65° |
9.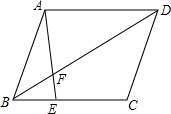 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )| A. | 4:5 | B. | 3:5 | C. | 4:9 | D. | 3:8 |
6.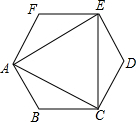 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )| A. | △ACE是等边三角形 | B. | 既是轴对称图形也是中心对称图形 | ||
| C. | 连接AD,则AD分别平分∠EAC与∠EDC | D. | 图中一共能画出3条对称轴 |
7.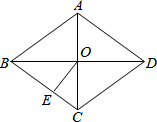 如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
 如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )| A. | S=AC•BD | B. | S=4BC•OE | C. | S=2AB•OE | D. | S=2BD•AO |
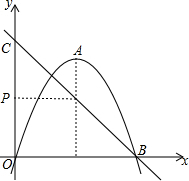 如图,抛物线y=-(x+m)2+k的顶点A的坐标为(2,4),与x轴的正半轴交于点B,点C的坐标为(0,4),点A,P关于直线BC对称.
如图,抛物线y=-(x+m)2+k的顶点A的坐标为(2,4),与x轴的正半轴交于点B,点C的坐标为(0,4),点A,P关于直线BC对称.