题目内容

17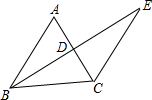．如图，BE⊥AC于点D，且AD=CD，BD=ED，若∠A=54°，求∠E的度数．

分析 根据BE⊥AC，∠ABD=90°-∠A=36°，再证明△ABD≌△CED，推出∠E=∠ABD即可．

解答 解：∵BE⊥AC，
∴∠ADB=∠BDC=90°，
∵∠A=54°，
∴∠ABD=90°-∠A=36°，
在△ABD和△CED中，
$\left\{\begin{array}{l}{AD=CD}\\{∠ADB=∠EDC}\\{BD=ED}\end{array}\right.$，
∴△ABD≌△CED（SAS），
∴∠E=∠ABD=36°．

点评 本题考查了等腰三角形性质，全等三角形的性质和判定的应用，关键是求出∠ABD度数和求出∠E=∠ABD．

练习册系列答案
相关题目
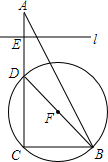7．如图，在Rt△ABC中，∠C=90°，AC=4，BC=2，D、E两点分别从顶点C、A沿着AC边向点A、C运动，点D的速度为1个单位/秒，点E的速度为2个单位/秒．以BD为直径作⊙F，过点E作CB边的平行线l，问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切．
8．在数轴上，表示-2与-6的点之间的距离是4个单位长度．
5．在班委会干部选举中，某同学的票没有超过半数，这是指这位同学的票是频率（　　）
A．大于0.5B．等于0.5C．小于或等于0.5D．大于或等于0.5
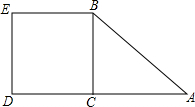12．如图，已知Rt△ABC中，∠ACB=90°，AB=10cm，AC=8cm，则正方形BCDE的面积是36cm2．
2．已知抛物线y=（x-1）2-4的顶点为（1，-4）．
①将它沿直线y=$\frac{1}{2}$翻折，求翻折后的顶点坐标；
②将它沿直线y=-$\frac{3}{2}$翻折，求翻折后的顶点坐标．
9．如图，AB、CD为⊙O的两条弦，AB=CD．求证：∠AOC=∠BOD．
6．阅读下面材料：点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a-b|，当A、B两点都不在原点时，

点A、B都在原点的右边，如图2，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
点A、B在原点的左边，如图3，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；
点A、B在原点的两边，如图4，|AB|=|OA|+|OB|=|a|+|b|=a+（-b）=|a-b|．
综上，数轴上A、B两点的距离|AB|=|a-b|．
回答下列问题：
（1）数轴上表示2和5的两点之间的距离是3，数轴上表示-2和-5的两点之间的距离是3，数轴上表示1和-3的两点之间的距离是4；
（2）数轴上表示x和-1的两点A和B之间的距离是|x+1|，如果|AB|=2那么x为1或-3．
（3）当代数式|x+1|+|x-2|取最小值时，相应x的取值范围是-1≤x≤2．
7．已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=6，则此梯形的周长为（　　）
A．16B．18C．20D．22

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网