题目内容
9. 如图,AB、CD为⊙O的两条弦,AB=CD.求证:∠AOC=∠BOD.
如图,AB、CD为⊙O的两条弦,AB=CD.求证:∠AOC=∠BOD.
分析 因为弦AB=CD,所以$\widehat{AB}$=$\widehat{CD}$;然后根据圆心角、弧、弦的关系定理,可以证得∠AOC=∠BOD.
解答  解:∵弦AB=CD(已知),
解:∵弦AB=CD(已知),
∴$\widehat{AB}$=$\widehat{CD}$;
∴∠AOB=∠COD,
∴∠AOB-∠BOC=∠COD-∠BOC,
即∠AOC=∠BOD.
点评 本题运用圆心角、弧、弦的关系定理解题,在同圆或等圆中,如果①两个圆心角,②两条弦,③两条弧,④两条弦的弦心距中,有任意一组量相等,其他各组量都相等.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.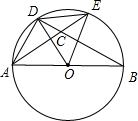 如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
 如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 个 |
20.在实数:5.2,-$\frac{2}{3}$,0.028,$\sqrt{3}$,$\root{3}{10}$,3$\frac{1}{2}$,3.14中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列说法正确的是( )
| A. | 对角线相等且互相垂直的四边形是菱形 | |
| B. | 对角线互相垂直的平行四边形是正方形 | |
| C. | 对角线相等且互相平分的四边形是矩形 | |
| D. | 对角线互相垂直的菱形是正方形 |
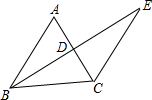 如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.
如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数. 一个立体图形是由若干个小正方体堆积而成的,其三视图如图,则组成这个立体图形的小正方体有多少个.
一个立体图形是由若干个小正方体堆积而成的,其三视图如图,则组成这个立体图形的小正方体有多少个.