题目内容
7.已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=6,则此梯形的周长为( )| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
分析 根据题意画出图形,分别过点A、D作AE⊥BC,DF⊥BC,根据四边形ABCD是等腰梯形可知AB=CD,故BE=CF,再由AD=2,BC=6可求出BE的长,再由∠B=60°可求出AB的长,进而可得出结论.
解答  解:如图所示,过点A、D作AE⊥BC,DF⊥BC,
解:如图所示,过点A、D作AE⊥BC,DF⊥BC,
∵四边形ABCD是等腰梯形,
∴AB=CD,
∴BE=CF.
∵AD=2,BC=6,
∴BE=$\frac{6-2}{2}$=2.
∵∠B=60°,
∴AB=4,
∴此梯形的周长=2AB+AD+BC=2×4+2+6=16.
故选A.
点评 本题考查的是等腰梯形的性质,熟知根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
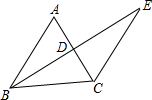 如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.
如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.