题目内容
7.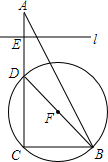 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E两点分别从顶点C、A沿着AC边向点A、C运动,点D的速度为1个单位/秒,点E的速度为2个单位/秒.以BD为直径作⊙F,过点E作CB边的平行线l,问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E两点分别从顶点C、A沿着AC边向点A、C运动,点D的速度为1个单位/秒,点E的速度为2个单位/秒.以BD为直径作⊙F,过点E作CB边的平行线l,问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.
分析 作FG⊥CD于G,FH⊥BC于H,设t秒钟后直线l与⊙F相切.根据勾股定理求得⊙F的半径,进而根据切线的性质,得出:2t+$\sqrt{(\frac{t}{2})^{2}+{1}^{2}}$+$\frac{1}{2}$t=4,解方程即可求得t的值.
解答 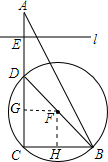 解:作FG⊥CD于G,FH⊥BC于H,设t秒钟后直线l与⊙F相切.
解:作FG⊥CD于G,FH⊥BC于H,设t秒钟后直线l与⊙F相切.
∴CD=t,AE=2t,
∴CG=DG=$\frac{1}{2}$CD=$\frac{1}{2}$t,CH=BH=$\frac{1}{2}$BC=1,
∵BC⊥AC,
∴GF∥BC,
∵DF=BF,
∴GF=$\frac{1}{2}$BC=1,
∴四边形CHFG是矩形,
∴FH=GC=$\frac{1}{2}$t,
在Rt△DGF中,DF=$\sqrt{DG^2+GF^2}$=$\sqrt{(\frac{t}{2})^{2}+{1}^{2}}$,
根据题意:2t+$\sqrt{(\frac{t}{2})^{2}+{1}^{2}}$+$\frac{1}{2}$t=4,
解得t1=$\frac{10+\sqrt{10}}{6}$(舍去),t=$\frac{10-\sqrt{10}}{6}$,
∴$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.
故答案为$\frac{10-\sqrt{10}}{6}$.
点评 本题考查了切线的性质,勾股定理的应用,根据题意得出2t+$\sqrt{(\frac{t}{2})^{2}+{1}^{2}}$+$\frac{1}{2}$t=4是解题的关键.

练习册系列答案
相关题目
19.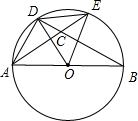 如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
 如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 个 |
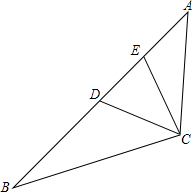 已知,在△ABC中,AB=2AC,D为AB中点,E为AD的中点,求证:BC=2CE.
已知,在△ABC中,AB=2AC,D为AB中点,E为AD的中点,求证:BC=2CE.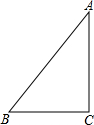 如图是一个直角三角形纸片,其中∠C=90°,两直角边长分别为3cm,4cm,现要给这个纸片再拼接一个直角三角形纸片,两纸片不重叠且无缝隙,使得拼接后的纸片形状是等腰三角形,拼接成的等腰三角形的纸片的周长为16或18cm.
如图是一个直角三角形纸片,其中∠C=90°,两直角边长分别为3cm,4cm,现要给这个纸片再拼接一个直角三角形纸片,两纸片不重叠且无缝隙,使得拼接后的纸片形状是等腰三角形,拼接成的等腰三角形的纸片的周长为16或18cm.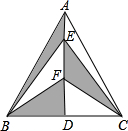 如图,在面积为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是2$\sqrt{3}$.
如图,在面积为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是2$\sqrt{3}$.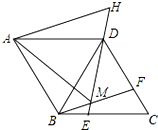 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
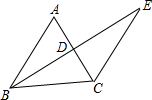 如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.
如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.