Question

8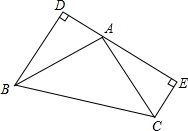．如图，BD⊥DE于D，CE⊥DE于E，AD=CE=2，BD=AE=4．
 （1）直接写出梯形BDEC的面积为6．
 （2）求证：AB=AC．
 （3）求AB的长．

Answer 1

分析 （1）根据全等三角形的判定证明△ADB与△CEA全等，再利用全等三角形的性质和梯形的面积公式计算即可；
（2）根据全等三角形的判定证明△ADB与△CEA，再利用全等三角形的性质证明即可；
（3）根据勾股定理解答即可．

解答 解：（1）∵BD⊥DE于D，CE⊥DE于E，
∴∠BDA=∠AEC=90°，
∴梯形BDEC的面积=$\frac{（2+4）（2+4）}{2}=6$，
故答案为：6；
（2）∵BD⊥DE于D，CE⊥DE于E，
∴∠BDA=∠AEC=90°，
在△ADB与△CEA中
$\left\{\begin{array}{l}{BD=AE}\\{∠BDA=∠AEC}\\{AD=CE}\end{array}\right.$
∴△ADB≌△CEA（SAS），
∴AB=AC；
（3）在Rt△ADB中，AB=$\sqrt{A{D}^{2}+D{B}^{2}}=\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$

点评 此题考查全等三角形的判定和性质，关键根据全等三角形的判定证明△ADB与△CEA全等．