题目内容
20．已知点A（0，4），B点在x轴上，线段AB与坐标轴围成三角形的面积为2，则B点坐标为（ ）| A． | （1，0） | B． | （-1，0） | C． | （1，0）或（-1，0） | D． | （0，-1）或 （0，1） |
分析 根据三角形的面积，可得OB的长，可得B点坐标．
解答 解：由点A（0，4），B点在x轴上，线段AB与坐标轴围成三角形的面积为2，得
OB=1，
B（1，0）或（-1，0），
故选：C．
点评 本题考查了坐标与图形的性质，利用三角形的面积得出OB的长是解题关键，注意B点有两个坐标，以防遗漏．
练习册系列答案
相关题目
2．点C是线段AB上一点，D是线段BC的中点．若AD=5cm．则AC+AB等于（ ）
| A． | 8cm | B． | 10cm | C． | 12cm | D． | 不确定 |
如图，已知梯形ABCD中，∠A=∠B=90°，AB=AD=12cm，BC=21cm，CD=15cm，E是AD上的点，AE=8cm．
8．观察下列图形中点的个数，若按其规律再画下去，可以得到第5个图形中所有点的个数为（ ）
| A． | 16个 | B． | 25个 | C． | 36个 | D． | 49个 |
15．在Rt△ABC中，AD为斜边上的高，S△ABC=4S△ABD，则cosB=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{3}{5}$ | D． | $\frac{\sqrt{3}}{2}$ |
5．
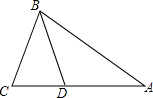如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，若AC=2a，则AD的长是（ ）
如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，若AC=2a，则AD的长是（ ）| A． | $\frac{\sqrt{5}-1}{2}$a | B． | $\frac{\sqrt{5}+1}{2}$a | C． | （$\sqrt{5}$-1）a | D． | （$\sqrt{5}$+1）a |
12．将抛物线y=x2+1先向左平移2个单位，再向下平移4个单位，那么所得到的抛物线的函数关系式是（ ）
| A． | y=（x+2）2+3 | B． | y=（x+2）2-3 | C． | y=（x-2）2+3 | D． | y=（x-2）2-3 |
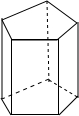如图所示的五棱柱的底面边长都是5cm，侧棱长12cm，它有多少个面？它的所有侧面的面积之和是多少？