题目内容
2. 如图,长方形ABCD中放置9个形状、大小都相同的小长方形,相关数据图中所示,则图中阴影部分的面积为多少.
如图,长方形ABCD中放置9个形状、大小都相同的小长方形,相关数据图中所示,则图中阴影部分的面积为多少.
分析 设小长方形的长为x,宽为y,根据图示可以列出方程组$\left\{\begin{array}{l}{x+4y=9}\\{x+2y-3y=4}\end{array}\right.$,然后解这个方程组即可求出小长方形的面积,接着就可以求出图中阴影部分的面积.
解答 解:设小长方形的长为x,宽为y,依题意有
$\left\{\begin{array}{l}{x+4y=9}\\{x+2y-3y=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$,
9×(4+1×3)-5×1×9
=9×7-45
=63-45
=18.
答:图中阴影部分的面积为18.
点评 此题主要考查了二元一次方程组的应用,此题是一个信息题目,要求学生会根据图示找出数量关系,根据图示可以列出两个方程,联立求出小长方形的长和宽.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设(2a+3b)2=(2a-3b)2+A,则A=( )
| A. | 6ab | B. | 12ab | C. | 0 | D. | 24ab |
11.下列各式由左边到右边的变形中,是分解因式的为( )
| A. | -xy2+2xy-3y=-y(xy-2x+3) | B. | 2x2-xy-x=2x(x-y-1) | ||
| C. | (y-2)2=y2-4y+4 | D. | x2-x-3=x(x-1)-3 |
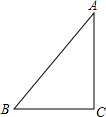 如图,将△ABC沿BC方向平移线段$\frac{1}{2}$BC的长度得到△DEF,点A与点D对应,点B与点E对应,画出平移后的图形并回答下列问题:
如图,将△ABC沿BC方向平移线段$\frac{1}{2}$BC的长度得到△DEF,点A与点D对应,点B与点E对应,画出平移后的图形并回答下列问题: