题目内容
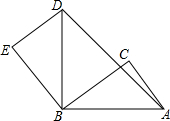 在△ABC中,∠C=90°,AC=3,BC=4,若将△ABC绕点B逆时针旋转90°后,点A的对应点为D,则AD的长为( )
在△ABC中,∠C=90°,AC=3,BC=4,若将△ABC绕点B逆时针旋转90°后,点A的对应点为D,则AD的长为( )A、5
| ||
B、3
| ||
C、4
| ||
| D、不确定 |
考点:旋转的性质
专题:
分析:由在△ABC中,∠C=90°,AC=3,BC=4,可求得AB的长,然后由将△ABC绕点B逆时针旋转90°后,点A的对应点为D,可得△ABD是等腰直角三角形,继而求得AD的长.
解答:解:∵在△ABC中,∠C=90°,AC=3,BC=4,
∴AB=
=5,
∵将△ABC绕点B逆时针旋转90°后,点A的对应点为D,
∴∠ABD=90°,AB=BD=5,
∴AD=
=5
.
故选A.
∴AB=
| AC2+BC2 |
∵将△ABC绕点B逆时针旋转90°后,点A的对应点为D,
∴∠ABD=90°,AB=BD=5,
∴AD=
| AB2+BD2 |
| 2 |
故选A.
点评:此题考查了旋转的性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
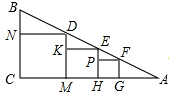 在Rt△ABC中,∠C=90°(如图),在△ABC中从左向右依次作内接正方形CNDM、正方形MKEH、正方形HPFG,若正方形CNDM的边长为m,正方形MKEH的边长为n,则正方形HPFG的边长可以表示为( )
在Rt△ABC中,∠C=90°(如图),在△ABC中从左向右依次作内接正方形CNDM、正方形MKEH、正方形HPFG,若正方形CNDM的边长为m,正方形MKEH的边长为n,则正方形HPFG的边长可以表示为( )A、
| ||
B、
| ||
| C、mn2 | ||
| D、m2n |
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A、爱 | B、的 | C、学 | D、美 |
 如图,在△ABC中,DE∥BC,若AD:AB=1:3,AC=9,则EC的长为
如图,在△ABC中,DE∥BC,若AD:AB=1:3,AC=9,则EC的长为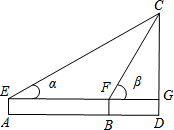 小红想要测量校园内一座教学楼CD的高度.她先在A处测得楼顶C的仰角α=30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角β=60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米)参考数据:
小红想要测量校园内一座教学楼CD的高度.她先在A处测得楼顶C的仰角α=30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角β=60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米)参考数据: 如图,直线AB、CD相交于点O,∠DOE=100°,∠AOC=30°,∠FOB=75°,求∠EOF的度数.
如图,直线AB、CD相交于点O,∠DOE=100°,∠AOC=30°,∠FOB=75°,求∠EOF的度数. 如图,已知AB是⊙O的直径,点C在⊙O上,若∠CAB=35°,求∠ABC的度数.
如图,已知AB是⊙O的直径,点C在⊙O上,若∠CAB=35°,求∠ABC的度数.