题目内容
如图，已知AB是⊙O的直径，点C在⊙O上，若∠CAB=35°，求∠ABC的度数．考点：圆周角定理
专题：
分析：由AB是⊙O的直径，根据直径所对的圆周角是直角，即可得∠C=90°，继而求得∠ABC的度数．
解答：解：∵AB是⊙O的直径，
∴∠C=90°，
∵∠CAB=35°，
∴∠ABC=90°-∠CAB=55°．
∴∠C=90°，
∵∠CAB=35°，
∴∠ABC=90°-∠CAB=55°．
点评：此题考查了圆周角定理．此题难度不大，注意掌握直径所对的圆周角是直角定理的应用是解此题的关键．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
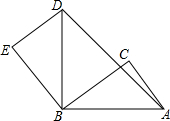在△ABC中，∠C=90°，AC=3，BC=4，若将△ABC绕点B逆时针旋转90°后，点A的对应点为D，则AD的长为（ ）A、5
| ||
B、3
| ||
C、4
| ||
| D、不确定 |
下列各式由左边到右边的变形中，是因式分解的为（ ）
| A、a（a+1）=a2+a |
| B、a2-2a-3=a（a-2）-3 |
| C、（a-b）x-（a-b）y=（a-b）（x-y） |
| D、（a+b）2-4ab=a2-2ab+b2 |
a，b，c，d，e是有理数，它们在数轴上的对应点的位置如图所示，把 a，b，c，d，e按照从小到大的顺序排列，得
某小区在绿化工程中有一块长为20m、宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为56m2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．
如图，在平面直角坐标系中，四边形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB，过点A的双曲线y=若把直线y=2x-3，向左平移3个单位长度，得到图象对应的函数解析式是（ ）
| A、y=2x |
| B、y=2x+3 |
| C、y=5x-3 |
| D、y=-x-3 |
下列计算正确的是（ ）
| A、（π-1）0=1 | ||||||
B、
| ||||||
C、（
| ||||||
D、
|