题目内容
6．已知y=$\sqrt{1-2x}$+$\sqrt{2x-1}$+$\sqrt{（x-1）^{2}}$，试求（4x-2y）2015的值．分析 由二次根式有意义的条件求得x的值，然后再求得y值，将x、y的值代入即可求得（4x-2y）2015的值．
解答 解：由二次根式有意义可知：1-2x≥0，2x-1≥0，
解得x=$\frac{1}{2}$．
将x=$\frac{1}{2}$代入得：y=$\frac{1}{2}$，
∴原式=12015=1．
点评 本题主要考查的是二次根式有意义的条件，根据二次根式有意义求得x、y的值是解题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
1．二次函数y=5（x-1）2的图象上有三点A（$\sqrt{2}$，y1），B（2，y2），C（-$\sqrt{5}$，y3），则y1、y2、y3的大小关系是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y3＞y1＞y2 | D． | y3＞y2＞y1 |
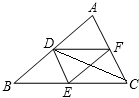如图所示，在△ABC中，D，E，F分别为边AB，BC，CA的中点，连接DE，DF，CD，EF，请你判断CD和EF的位置关系，并证明．
如图，分别以Rt△ABC的斜边AB，直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，DE，AB相交于点G，若∠BAC=30°，下列结论：①EF⊥AC；②四边形ADFE为平行四边形；③AD=4AG；④△DBF≌△EFA，其中正确结论的序号是（ ）