题目内容
16．
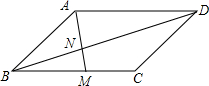如图，在?ABCD中，若M为BC边的中点，AM与BD交于点N，那么S△BMN：S?ABCD=（ ）| A． | 1：12 | B． | 1：9 | C． | 1：8 | D． | 1：6 |
分析 根据平行四边形的性质得出AD=BC，AD∥BC，求出BC=2BM=AD，根据相似三角形的判定得出△AND∽△MNB，求出DN：BN=AD：BM=2：1，根据相似三角形的性质和三角形的面积公式求出S△ABN=2S△BMN，S△AND=4S△BMN，即可得出答案．
解答 解：∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∵M为BC边的中点，
∴BC=2BM=AD，
∵AD∥BC，
∴△AND∽△MNB，
∴DN：BN=AD：BM=2：1，
∴$\frac{{S}_{△BMN}}{{S}_{△AND}}$=（$\frac{1}{2}$）2=$\frac{1}{4}$，$\frac{{S}_{△ABN}}{{S}_{△BMN}}$=2，
∴S△ABN=2S△BMN，S△AND=4S△BMN，
∴S平行四边形ABCD=2S△ABD=2（S△AND+S△ABN）=12S△BMN，
即S△BMN：S?ABCD=1：12，
故选A．
点评 本题考查了平行四边形的性质，相似三角形的性质和判定的应用，能灵活运用定理进行变形是解此题的关键，注意：相似三角形的面积之比等于相似比的平方．
练习册系列答案
相关题目
11．若二次根式$\sqrt{x-1}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≤-1 | B． | x≥-1 | C． | x≤1 | D． | x≥1 |
1．
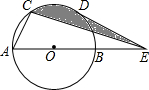如图所示，在半径为2cm的⊙O中，点C、点D是弧AB的三等分点，点E是直径AB的延长线上一点，连结CE、DE，则图中阴影部分的面积是（ ）
如图所示，在半径为2cm的⊙O中，点C、点D是弧AB的三等分点，点E是直径AB的延长线上一点，连结CE、DE，则图中阴影部分的面积是（ ）| A． | $\sqrt{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{2π}{3}-\sqrt{3}$ | D． | $\frac{2π}{3}$+$\sqrt{3}$ |
8．
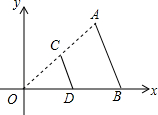如图，线段AB两个端点的坐标分别为A（6，6），B（8，0），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（ ）
如图，线段AB两个端点的坐标分别为A（6，6），B（8，0），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（ ）| A． | （3，0） | B． | （4，0） | C． | （3，3） | D． | （4，3） |
5．
如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m-n等于（ ）
如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m-n等于（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 无法确定 |
6．（-2）×3的结果是（ ）
| A． | 6 | B． | -6 | C． | 1 | D． | -5 |