题目内容
1.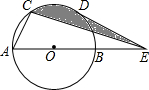 如图所示,在半径为2cm的⊙O中,点C、点D是弧AB的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )
如图所示,在半径为2cm的⊙O中,点C、点D是弧AB的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )| A. | $\sqrt{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{2π}{3}-\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
分析 首先连接OC、OD,易得△COD是等边三角形,又由CD∥AB,可得S△CED=S△COD,即可得S阴影=S扇形COD.
解答  解:连接OC、OD、CD,
解:连接OC、OD、CD,
∵C、D是半圆AB的两个三等分点,
∴∠DOB=∠COD=60°,
又∵CO=OD,
∴CO=OD=CD,
∴∠DOB=∠CDO=60°,
∴CD∥AB,
∴S△CED=S△COD,
∴S阴影=S扇形COD=$\frac{60×π×{2}^{2}}{360}$=$\frac{2}{3}$π(cm2),
故选B.
点评 本题主要考查了等边三角形的判定与性质以及扇形的面积.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
11.不等式组$\left\{\begin{array}{l}{x+1>2}\\{1-x≥-2}\end{array}\right.$的解集是( )
| A. | x<1 | B. | x≥3 | C. | 1≤x<3 | D. | 1<x≤3 |
16.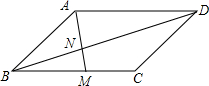 如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )
如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )
 如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )
如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )| A. | 1:12 | B. | 1:9 | C. | 1:8 | D. | 1:6 |
13.估计$\sqrt{11}$+1的值( )
| A. | 在2到3之间 | B. | 在3到4之间 | C. | 在4到5之间 | D. | 在5到6之间 |
10.一个底面半径是40cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为( )
| A. | 80° | B. | 160° | C. | 320° | D. | 100° |
11.在数$\frac{2}{3}$,1,-3,0中,绝对值最大的数是( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | -3 | D. | 0 |
 如图,直线y1=2x-1与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(-1,m).
如图,直线y1=2x-1与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(-1,m).