题目内容
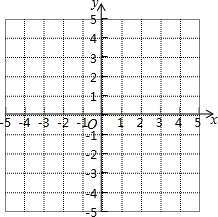 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为
(2)在所给的平面直角坐标系中画出此时抛物线;
(3)结合图象回答问题:当1<x<4时,y的取值范围是
考点:二次函数与不等式(组),二次函数的图象,抛物线与x轴的交点
专题:
分析:(1)根据函数值为零,可得函数图象与x轴的交点,根据自变量为零时,可得函数图象与y轴的交点,根据二次函数图象的顶点坐标公式,可得顶点坐标;
(2)根据描点法,可得函数图象;
(3)根据a=1>0,对称轴的右侧,y随x的增大而增大,可得答案.
(2)根据描点法,可得函数图象;
(3)根据a=1>0,对称轴的右侧,y随x的增大而增大,可得答案.
解答:
解:(1)它与x轴交点的坐标为 (1,0),(3,0),与y轴交点的坐标为 (0,3),顶点坐标为 (2,-1).
故答案为:(1,0),(3,0);(0,3);(2,-1);
(2)在所给的平面直角坐标系中画出此时抛物线: ,
,
(3)由图象,得
当1<x<4时,y的取值范围是-1<y<3.
故答案为:(1,0),(3,0);(0,3);(2,-1);
(2)在所给的平面直角坐标系中画出此时抛物线:
 ,
,(3)由图象,得
当1<x<4时,y的取值范围是-1<y<3.
点评:本题考查了二次函数与不等式的关系,利用了描点法画函数图象,利用了函数的性质.

练习册系列答案
相关题目
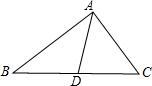 如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.
如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.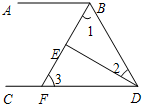 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.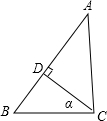 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设∠BCD=α,若sinα=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设∠BCD=α,若sinα=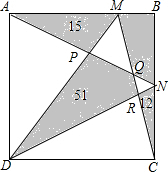 如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为
如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为 如图,正方形ABFG与正方形BCDE的面积之和为7,AD2-CG2=3,求AC•EF的值.
如图,正方形ABFG与正方形BCDE的面积之和为7,AD2-CG2=3,求AC•EF的值.