题目内容
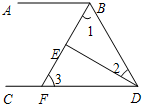 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.(1)试说明:AB∥CD;
(2)若∠2=25°,求∠3的度数.
考点:平行线的判定与性质
专题:
分析:(1)根据角平分线定义求出∠ABD+∠BDC=180°,根据平行线的判定推出即可;
(2)根据角平分线求出∠EDF,根据三角形外角性质求出∠FED,根据三角形内角和定理求出即可.
(2)根据角平分线求出∠EDF,根据三角形外角性质求出∠FED,根据三角形内角和定理求出即可.
解答:
解:(1)∵∠ABD和∠BDC的平分线交于E,
∴∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD;
(2)∵DE平分∠BDC,
∴∠EDF=∠2=25°,
∵∠1+∠2=90°,
∴∠FED=90°,
∴∠3=180°-90°-25°=65°.
∴∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD;
(2)∵DE平分∠BDC,
∴∠EDF=∠2=25°,
∵∠1+∠2=90°,
∴∠FED=90°,
∴∠3=180°-90°-25°=65°.
点评:本题考查了平行线的判定,三角形内角和定理,角平分线定义,三角形的外角性质的应用,能综合运用定理进行推理是解此题的关键,难度适中.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
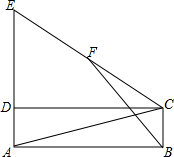 如图,在矩形ABCD中,延长AD至E,使AE=AC,F为CE的中点,连接BF.
如图,在矩形ABCD中,延长AD至E,使AE=AC,F为CE的中点,连接BF.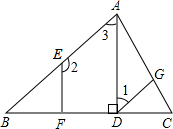 如图所示,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
如图所示,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.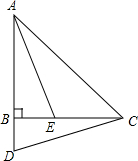 如图,△ABC是等腰直角三角形,∠ABC=90°,D是AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DC,∠BCD=15°,则∠AEC=
如图,△ABC是等腰直角三角形,∠ABC=90°,D是AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DC,∠BCD=15°,则∠AEC=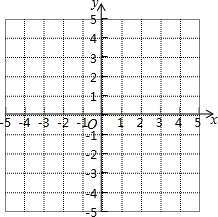 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.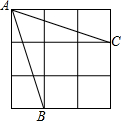 如图是一个3×3的正方形网格,那么tan∠BAC=
如图是一个3×3的正方形网格,那么tan∠BAC=