题目内容
 如图,正方形ABFG与正方形BCDE的面积之和为7,AD2-CG2=3,求AC•EF的值.
如图,正方形ABFG与正方形BCDE的面积之和为7,AD2-CG2=3,求AC•EF的值.考点:勾股定理,正方形的性质
专题:计算题
分析:在直角三角形ACD与直角三角形ACG中,利用勾股定理列出两个关系式,相减求出CD2-AG2=3,由两正方形的面积之和得到CD2+AG2=7,联立求出CD与AG的长,进而求出AC与EF的长,即可求出所求式子的值.
解答:
解:由图可知AD2=AC2+CD2①,CG2=AC2+AG2②,
①-②可得:AD2-CG2=CD2-AG2=3,
由正方形面积CD2+AG2=7,
解得:CD2=5,AG2=2,
即CD=
,AG=
,
∴AC=AB+BC=
+
,EF=EB-FB=
-
,
则AC•EF=(
+
)×(
-
)=5-2=3.
①-②可得:AD2-CG2=CD2-AG2=3,
由正方形面积CD2+AG2=7,
解得:CD2=5,AG2=2,
即CD=
| 5 |
| 2 |
∴AC=AB+BC=
| 5 |
| 2 |
| 5 |
| 2 |
则AC•EF=(
| 5 |
| 2 |
| 5 |
| 2 |
点评:此题考查了勾股定理,以及正方形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
下列命题中是真命题的是( )
| A、五边形的外角和等于360° |
| B、如果a+b>0,那么ab>0 |
| C、同位角相等 |
| D、一个锐角与一个钝角的和等于一个平角 |
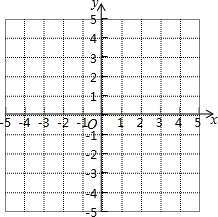 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为
(2)在所给的平面直角坐标系中画出此时抛物线;
(3)结合图象回答问题:当1<x<4时,y的取值范围是
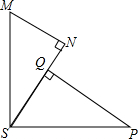 如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )
如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )| A、∠A=∠QSP |
| B、∠MSN=∠P |
| C、MS=SP |
| D、MN=QN |
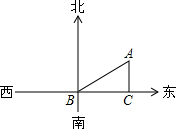 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)
一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)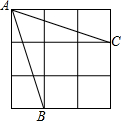 如图是一个3×3的正方形网格,那么tan∠BAC=
如图是一个3×3的正方形网格,那么tan∠BAC=