题目内容
关于x的多项式乘多项式(x2-3x-2)(ax+1),若结果中不含有x的一次项,求代数式:(2a+1)2-(2a+1)(2a-1)的值.
考点:多项式乘多项式
专题:
分析:原式利用多项式乘多项式法则计算,根据运算结果中不含x的一次项,求出a的值,再将(2a+1)2-(2a+1)(2a-1)化简后,把a的值代入即可.
解答:
解:原式=ax3-3ax2-2ax+x2-3x-2=ax3+(1-3a)x2-(2a+3)x-2,
由结果中不含x的一次项,得到-(2a+3)=0,
解得:a=-1.5,
(2a+1)2-(2a+1)(2a-1)
=4a2+4a+1-4a2+1
=4a+2
把a=-1.5代入4a+2=4×(-1.5)+2=-4,
所以(2a+1)2-(2a+1)(2a-1)的值为-4.
由结果中不含x的一次项,得到-(2a+3)=0,
解得:a=-1.5,
(2a+1)2-(2a+1)(2a-1)
=4a2+4a+1-4a2+1
=4a+2
把a=-1.5代入4a+2=4×(-1.5)+2=-4,
所以(2a+1)2-(2a+1)(2a-1)的值为-4.
点评:本题主要考查了多项式的乘法计算,理解结果中不含有x的一次项的意思是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
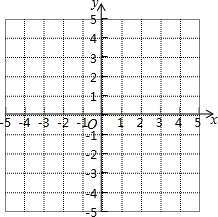 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为
(2)在所给的平面直角坐标系中画出此时抛物线;
(3)结合图象回答问题:当1<x<4时,y的取值范围是
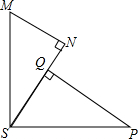 如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )
如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )| A、∠A=∠QSP |
| B、∠MSN=∠P |
| C、MS=SP |
| D、MN=QN |
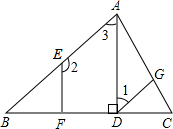 如图所示,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
如图所示,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.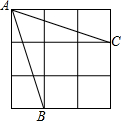 如图是一个3×3的正方形网格,那么tan∠BAC=
如图是一个3×3的正方形网格,那么tan∠BAC= 如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.
如图,△EDF中,∠EDF=90°,点B是EF的中点,点M在边ED上,过点B作MB的垂线交边DF于N点,求证:BM2+BN2=ME2+NF2.