题目内容
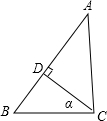 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设∠BCD=α,若sinα=
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设∠BCD=α,若sinα=| 3 |
| 5 |
考点:解直角三角形
专题:
分析:根据sinα=
,利用勾股定理即可得出CD,再根据同角的余角相等得∠ACD=∠B,根据三角函数的定义,即可得出答案.
| 3 |
| 5 |
解答:
解:∵sinα=
,
∴设BD=3x,BC=5x,
∴CD=4x,
∵∠ACD+∠α=∠B+α=90°,
∴∠ACD=∠B,
∴sin∠ACD=sin∠B=
=
=
.
| 3 |
| 5 |
∴设BD=3x,BC=5x,
∴CD=4x,
∵∠ACD+∠α=∠B+α=90°,
∴∠ACD=∠B,
∴sin∠ACD=sin∠B=
| CD |
| BC |
| 4x |
| 5x |
| 4 |
| 5 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了勾股定理.

练习册系列答案
相关题目
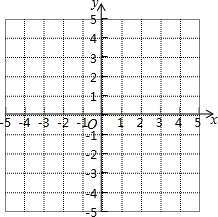 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为
(2)在所给的平面直角坐标系中画出此时抛物线;
(3)结合图象回答问题:当1<x<4时,y的取值范围是
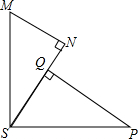 如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )
如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,添加下列条件能使△MNS≌△SQP的是( )| A、∠A=∠QSP |
| B、∠MSN=∠P |
| C、MS=SP |
| D、MN=QN |
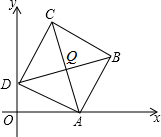 如图,正方形ABCD的顶点A、D的坐标分别为(8,0)、(0,6),对角线AC、BD交于Q,则点Q的坐标为
如图,正方形ABCD的顶点A、D的坐标分别为(8,0)、(0,6),对角线AC、BD交于Q,则点Q的坐标为 如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是
如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是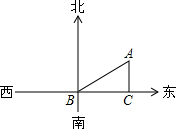 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)
一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,求这艘船航行的速度.(精确到1海里/时)