题目内容
4.阅读下列解题过程:、已知a、b、c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4,①
所以c2(a2-b2)=(a2-b2)(a2+b2)②.
所以c2=a2+b2.③
所以△ABC是直角三角形.④
请你判断上述解题过程是否正确?如果有误,请你将正确的解答过程写下来.
分析 利用提公因式法把原式因式分解,根据等腰三角形的判定、勾股定理的逆定理解答.
解答 解:上述解题过程不正确,
∵a2c2-b2c2=a4-b4,
∴c2(a2-b2)=(a2-b2)(a2+b2),
∴(a2-b2)(c2-a2+b2)=0,
∴a2-b2=0或(c2-a2+b2)=0,
∴a=b或c2=a2+b2,
∴△ABC是等腰三角形或直角三角形.
点评 本题考查的是勾股定理的逆定理的应用以及因式分解的应用,掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各图中,正确画出AC边上的高的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
 如图,△ABC内接于⊙O,∠ABC=60°,D为$\widehat{AC}$的中点.若CD=1,则⊙O的直径为2.
如图,△ABC内接于⊙O,∠ABC=60°,D为$\widehat{AC}$的中点.若CD=1,则⊙O的直径为2. 已知:如图,用长为18m的篱笆(3AB+BC),围成矩形花圃.一面利用墙(墙足够长),则围成的矩形花圃ABCD的占地面积最大为27m2.
已知:如图,用长为18m的篱笆(3AB+BC),围成矩形花圃.一面利用墙(墙足够长),则围成的矩形花圃ABCD的占地面积最大为27m2.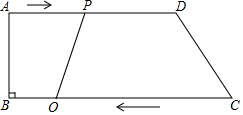 如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.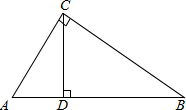 已知:如图,在Rt△ABC中,CD是斜边AB上高,找出图中的相似三角形.并说明理由.
已知:如图,在Rt△ABC中,CD是斜边AB上高,找出图中的相似三角形.并说明理由.