题目内容
9.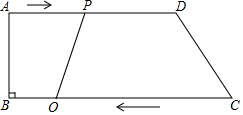 如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.(1)当t为何值时,四边形PQCD是平行四边形?
(2)当t为何值时,四边形PQBA是平行四边形?
(3)当四边形PQBA是平行四边形时,连接AQ,AB=$\sqrt{30}$.求AQ长.
分析 (1)设经过ts时,四边形PQCD是平行四边形,根据DP=CQ,代入后求出即可;
(2)设经过ts时,四边形PQBA是矩形,根据AP=BQ,代入后求出即可;
(3)由勾股定理即可求得结论.
解答 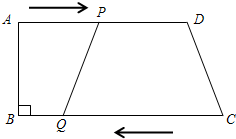 解:(1)设经过ts时,四边形PQCD是平行四边形,
解:(1)设经过ts时,四边形PQCD是平行四边形,
∵AP=t,CQ=3t,DP=24-t,
∴DP=CQ,
∴24-t=3t,
t=6,
即经过6s时,四边形PQCD是平行四边形;
(2)设经过ts时,四边形PQBA是平行四边形,
∵AP=t,CQ=3t,BQ=26-3t,
∴AP=BQ,
∴26-3t=t,
t=$\frac{13}{2}$,
即经过$\frac{13}{2}$s时,四边形PQBA是平行四边形;
(3)∵四边形PQCD是平行四边形,BQ=26-3t=26-3×$\frac{13}{2}$=$\frac{13}{2}$,∠ABQ=90°,
∴AQ=$\sqrt{A{B}^{2}+B{Q}^{2}}$=$\sqrt{(\sqrt{30})^{2}+(\frac{13}{2})^{2}}$=$\frac{17}{2}$(cm).
点评 此题主要考查勾股定理和平行四边形的判定掌握情况,本题解题关键是找出等量关系即可得解.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
18.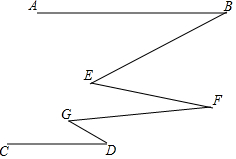 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )| A. | ∠D=∠F=∠B | B. | ∠B+∠F+∠D=60° | C. | ∠B+∠F+∠D=120° | D. | GD∥EF |
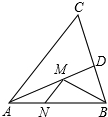 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.