题目内容
14．
如图，△ABC内接于⊙O，∠ABC=60°，D为$\widehat{AC}$的中点．若CD=1，则⊙O的直径为2．
分析 直接利用圆周角定理结合D为$\widehat{AC}$的中点得出∠DOC的度数，再利用等边三角形的判定与性质得出答案．
解答 
解：连接AO，DO，CO，
∵∠ABC=60°，
∴∠AOC=120°，
∵D为$\widehat{AC}$的中点，
∴∠DOC=∠AOD=60°，
∴△ODC是等边三角形，
∴CO=DC=DO=1，
∴⊙O的直径为2．
故答案为：2．
点评 此题主要考查了圆周角定理以及等边三角形的判定与性质，正确得出△ODC是等边三角形是解题关键．
练习册系列答案
相关题目
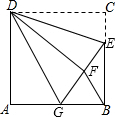如图，正方形ABCD的边长为12，点E在边BC上，且BE=2CE．将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连结DG，BF．下列结论：①△DAG≌△DFG；②DG∥BF；③EG=10；④S△BEF=9.6．其中所有正确结论的序号是①②③④（填序号）
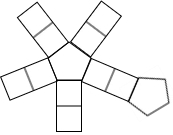“磁力健构片”通过磁铁连接重心，可以轻松制作成球体、锥体、正方体等百种造型，立体提拉魔幻成型，直观立体，是全面开发脑力的益智玩具．如图所示的平面图形经过立体提拉后，会成型为（ ）
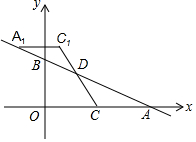如图，一次函数y=-$\frac{1}{2}$x+m（m＞0）的图象与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D．
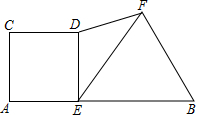如图，已知线段AB=10，点E在线段AB上运动（不与A、B重合），分别以AE、EB为边在AB的同侧作正方形ACDE和等边△BEF，连接DF，则DF2的最小值为50-25$\sqrt{3}$．