题目内容
12.课堂上老师讲解了比较$\sqrt{11}$-$\sqrt{10}$和$\sqrt{15}$-$\sqrt{14}$大小的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:$\frac{1}{\sqrt{11}-\sqrt{10}}$=$\sqrt{11}$+$\sqrt{10}$,而$\frac{1}{\sqrt{15}+\sqrt{14}}$=$\sqrt{15}$+$\sqrt{14}$.因为$\sqrt{15}$+$\sqrt{14}$>$\sqrt{11}$+$\sqrt{10}$,所以$\frac{1}{\sqrt{15}-\sqrt{14}}$>$\frac{1}{\sqrt{11}-\sqrt{10}}$,于是,必有$\sqrt{15}$-$\sqrt{14}$<$\sqrt{11}$-$\sqrt{10}$,根据上面介绍的方法,你能知道$\sqrt{2015}$-$\sqrt{2014}$与$\sqrt{2014}$-$\sqrt{2013}$谁大谁小吗?请你开动脑筋,并设计一种方法来比较$\sqrt{8}$+$\sqrt{3}$与$\sqrt{6}$+$\sqrt{5}$的大小.(不能用计算器哟!)分析 直接利用倒数的定义结合例题求出两数的倒数,进而比较得出答案;再利用两数平方进而比较得出答案.
解答 解:∵$\frac{1}{\sqrt{2015}-\sqrt{2014}}$=$\frac{\sqrt{2015}+\sqrt{2014}}{(\sqrt{2015}-\sqrt{2014})(\sqrt{2015}+\sqrt{2014})}$=$\sqrt{2015}$+$\sqrt{2014}$,
可得:$\frac{1}{\sqrt{2014}-\sqrt{2013}}$=$\sqrt{2014}$+$\sqrt{2013}$,
∵$\sqrt{2015}$+$\sqrt{2014}$>$\sqrt{2014}$+$\sqrt{2013}$,
∴$\frac{1}{\sqrt{2015}-\sqrt{2014}}$>$\frac{1}{\sqrt{2014}-\sqrt{2013}}$,
∴$\sqrt{2015}$-$\sqrt{2014}$<$\sqrt{2014}$-$\sqrt{2013}$;
∵($\sqrt{8}$+$\sqrt{3}$)2=8+3+2$\sqrt{24}$=11+2$\sqrt{24}$,
($\sqrt{6}$+$\sqrt{5}$)2=6+5+2$\sqrt{30}$=11+2$\sqrt{30}$,
显然$\sqrt{30}$>$\sqrt{24}$,
所以($\sqrt{6}$+$\sqrt{5}$)2>($\sqrt{8}$+$\sqrt{3}$)2,
又∵$\sqrt{6}$+$\sqrt{5}$>0,$\sqrt{8}$+$\sqrt{3}$>0
∴$\sqrt{6}$+$\sqrt{5}$>$\sqrt{8}$+$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.




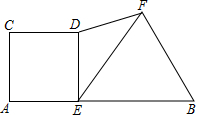 如图,已知线段AB=10,点E在线段AB上运动(不与A、B重合),分别以AE、EB为边在AB的同侧作正方形ACDE和等边△BEF,连接DF,则DF2的最小值为50-25$\sqrt{3}$.
如图,已知线段AB=10,点E在线段AB上运动(不与A、B重合),分别以AE、EB为边在AB的同侧作正方形ACDE和等边△BEF,连接DF,则DF2的最小值为50-25$\sqrt{3}$.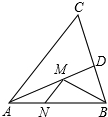 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.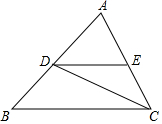 已知如图,在△ABC中,2∠B=∠ACB,给出下列3个条件
已知如图,在△ABC中,2∠B=∠ACB,给出下列3个条件