Question

8．在△ABC中，AB=AC，AD，CE分别平分∠BAC和∠ACB，且AD与CE交于点M．点N在射线AD上，且NA=NC．过点N作NF⊥CE于点G，且与AC交于点F，再过点F作FH∥CE，且与AB交于点H．

（1）如图1，当∠BAC=60°时，点M，N，G重合．
①请根据题目要求在图1中补全图形；
②连结EF，HM，则EF与HM的数量关系是EF=HM；
（2）如图2，当∠BAC=120°时，求证：AF=EH．

Answer 1

分析 （1）①根据条件可补全图形，如图1①；②连接MF，如图1②，要证EF=HM，由于点M，N重合，只需证到EF=HN，只需证到四边形ENFH是矩形即可．
（2）连接FM，EF，如图2．易证△ANC是等边三角形，从而有AN=AC．进而可证到△AFN≌△AMC，则有AF=AM，从而得到△AMF是等边三角形，则有AF=FM，∠AMF=60°．进而可证到四边形FHEM是平行四边形，则有EH=FM，即AF=EH．

解答 解：（1）①补全图形，如图1①．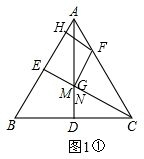
②连接MF，EF，如图1②．
∵AB=AC，∠BAC=60°，
∴△ABC是等边三角形，
∴CA=CB．
∵CE平分∠ACB，
∴CE⊥AB，即∠AEC=90°．
∵NF⊥CE，即∠FNC=90°，
∴∠AEC=∠FNC，
∴EH∥FN．
∵FH∥CE，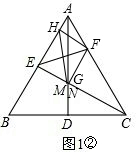
∴四边形ENFH是平行四边形．
∵∠AEC=90°，
∴平行四边形ENFH是矩形．
∴EF=HN．
∵点M，N重合，
∴EF=HM．
故答案为：EF=HM．

（2）连接FM，如图2．
∵AD，CE分别平分∠BAC和∠ACB，且∠BAC=120°，
∴∠BAD=∠CAD=60°，∠ACE=∠BCE．
∵AB=AC，∴AD⊥BC．
∵NG⊥EC，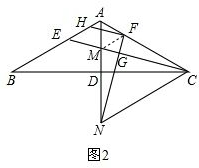
∴∠MDC=∠NGM=90°，
∴∠BCE+∠DMC=90°，∠MNG+∠DMC=90°．
∴∠BCE=∠MNG．
∴∠ACE=∠MNG．
∵NA=NC，∠NAC=60°，
∴△ANC是等边三角形，
∴AN=AC．
在△AFN和△AMC中，
$\left\{\begin{array}{l}{∠ANF=∠ACM}\\{AN=AC}\\{∠NAF=∠CAM}\end{array}\right.$，
∴△AFN≌△AMC（ASA），
∴AF=AM．
∴△AMF是等边三角形．
∴AF=FM，∠AMF=60°．
∴∠AMF=∠BAD．
∴FM∥AE．
∵FH∥CE，
∴四边形FHEM是平行四边形．
∴EH=FM．
∴AF=EH．

点评 本题考查了黄金三角形、全等三角形的判定与性质、等边三角形的判定与性质、矩形的判定与性质、平行四边形的判定与性质、垂直平分线的性质、平行线分线段成比例等知识，综合性比较强，有一定的难度．