题目内容
4. 某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:
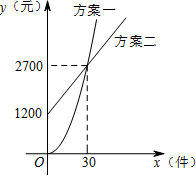
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点在原点的抛物线的一部分,方案二所示的图形是射线.设推销员销售产品的数量为x(件),付给推销员的月报酬为y(元).
(1)分别求两种方案中y关于x的函数关系式;
(2)当销售量达到多少件时,两种方案的月报酬差额将达到3 800元?
(3)若公司决定改进“方案二”:基本工资1 200元,每销售一件产品再增加报酬m元,当推销员销售量达到40件时,方案二的月报酬不低于方案一的月报酬.求m至少增加多少元?
分析 (1)分别设出两种方案中y关于x的函数关系式,用待定系数法求解,即可解答;
(2)根据“两种方案月报酬差额将达到3800元”,得到方程30x2-(50x+1200)=3800,即可解答;
(3)分别计算出当销售员销售产量达到40件时,方案一与方案二的月报酬,根据方案二的月报酬不低于方案一的月报酬,列出不等式组,即可解答.
解答 解:(1)设y1=ax2,
把(30,2700)代入得:900a=2700,
解得:a=3,
∴y1=3x2.
设y2=kx+b,
把(0,1200),(30,2700)代入得:$\left\{\begin{array}{l}{b=1200}\\{30k+b=2700}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=50}\\{b=1200}\end{array}\right.$,
∴y2=50x+1200.
(2)由题意得:30x2-(50x+1200)=3800,
解得:x1=50,x2=-$\frac{100}{3}$(舍去),
答:当销售达到50件时,两种方案月报酬差额将达到3800元.
(3)当销售员销售产量达到40件时,
方案一的月报酬为:3×402=4800,
方案二的月报酬为:(50+m)×40+1200=40m+3200,
由题意得:40m+3200≥4800,
解得:m≥40,
答:当推销员销售量达到40件时,方案二的月报酬不低于方案一的月报酬,m至少增加40元.
点评 本题主要考查二次函数、一元二次方程及一元一次不等式的实际应用能力,根据题意准确抓住相等关系和不等关系是列函数解析式、方程或不等式的关键.

练习册系列答案
相关题目
19.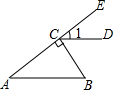 如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )
如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )
 如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )
如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
16.下列各组的两项是同类项的为( )
| A. | 3m2n2与-m2n3 | B. | $\frac{1}{2}$xy与2yx | C. | 53与a3 | D. | 3x2y2与4x2z2 |
14.不等式组$\left\{\begin{array}{l}{2x+1<3}\\{4x>1}\end{array}\right.$的解集是( )
| A. | x>1 | B. | x<$\frac{1}{4}$ | C. | $\frac{1}{4}$<x<1 | D. | 无解 |

 如果两个变量x、y之间的函数关系如图所示,则自变量x的取值范围是-3≤x≤3.
如果两个变量x、y之间的函数关系如图所示,则自变量x的取值范围是-3≤x≤3.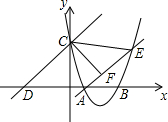 如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.