Question

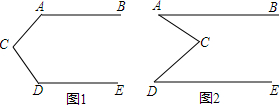
1．已知：如图，AB∥DE
（1）如图1，点C在直线AB和DE之间且在线段AD左侧时，猜测∠A、∠ACD、∠D有什么关系，并证明你的结论；
（2）如图2，点C在直线AB和DE之间，且点C向右移动到线段AD的右侧，此时∠A、∠ACD、∠D之间有什么样的关系？请你写出正确的结论并证明．

Answer 1

分析 （1）首先过点C作CM∥AB，由AB∥DE，可得AB∥CM∥DE，根据两直线平行，同旁内角互补，即可得∠A+∠ACM=180°，∠MCD+∠D=180°，继而求得答案；
（2）过点C作CM∥AB，由AB∥DE，可得AB∥CM∥DE，然后由两直线平行，内错角相等，即可求得答案．

解答 解：（1）∠A+∠ACD+∠D=360°．
证明：如图1，过点C作CM∥AB，
∵AB∥DE，
∴AB∥CM∥DE，
∴∠A+∠ACM=180°，∠MCD+∠D=180°，
∴∠A+∠ACD+∠D=360°．

（2）不符合（1）中的结论．
正确的结论是：∠ACD=∠A+∠D，
证明：过点C作CN∥AB，
∵AB∥DE，
∴AB∥CN∥DE，
∴∠A=∠ACN，∠D=∠DCN，
∴∠ACD=∠ACN+∠DCN=∠A+∠D．

点评 本题考查了平行线的性质，正确作出辅助线是解题的关键．