题目内容
10. 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D.若AD、BD是关于x的方程x2-10x+m=0的两个根,且S△ABC=20,求m的值?
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D.若AD、BD是关于x的方程x2-10x+m=0的两个根,且S△ABC=20,求m的值?
分析 利用一元二次方程的根与系数的关系及相似三角形的性质求得CD的长,再根据直角三角形高与斜边的关系求得m的长.
解答 解:∵AD、DB的长是方程x2-10x+m=0的根,
∴AD+DB=AB=10,AD•DB=m;
∵△ABC的面积为20,
∴S△ABC=$\frac{1}{2}$CD•AB=$\frac{1}{2}$CD×10=20;
∴CD=4;
∵在直角△ABC中,Rt△ADC∽Rt△CDB,
∴CD:BD=AD:CD;
∴CD2=AD•DB=m=16,
∴m=16.
点评 本题考查了射影定理,一元二次方程的根与系数的关系,直角三角形的性质,相似三角形的性质,直角三角形的面积公式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
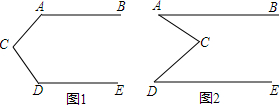
 如图,已知直线l及l两侧的两点A、B.
如图,已知直线l及l两侧的两点A、B. 如图所示,某地下车库的人口处有一斜坡AB,其坡度i=1:1.5,则斜坡AB的长为$\sqrt{13}$m.
如图所示,某地下车库的人口处有一斜坡AB,其坡度i=1:1.5,则斜坡AB的长为$\sqrt{13}$m. 旋转均匀转盘甲和转盘乙(如图),如果你想让指针停在蓝色上,那么选哪个转盘能使你成功的可能性比较大?
旋转均匀转盘甲和转盘乙(如图),如果你想让指针停在蓝色上,那么选哪个转盘能使你成功的可能性比较大? (1)如第2幅图所示,在2×2的方格中共几个正方形?图中有2×2个
(1)如第2幅图所示,在2×2的方格中共几个正方形?图中有2×2个 ,1×1个
,1×1个 ,共2×2+1×1=5个正方形;
,共2×2+1×1=5个正方形; ,共14个正方形;
,共14个正方形; ,共30个正方形.
,共30个正方形.