题目内容
如图1,抛物线y=-x2+2bx+c(b>0)与y轴交于点C,点P为抛物线顶点,分别作点P,C关于原点O的对称点P′,C′,顺次连接四点得四边形PC P′C′.
(1)当b=c=1时,求顶点P的坐标;
(2)当b=2,四边形PC P′C′为矩形时(如图2),求c的值;
(3)请你探究:四边形PCP′C′能否成为正方形?若能,求出符合条件的b,c的值;若不能,请说明理由.

(1)当b=c=1时,求顶点P的坐标;
(2)当b=2,四边形PC P′C′为矩形时(如图2),求c的值;
(3)请你探究:四边形PCP′C′能否成为正方形?若能,求出符合条件的b,c的值;若不能,请说明理由.

考点:二次函数综合题
专题:
分析:(1)当b=c=1时,直接代入再利用配方法求出顶点坐标即可;
(2)当b=2时,y=-x2+2bx+c=-x2+4x+c=-(x-2)2+4+c,则顶点P的坐标为(2,4+c),再利用矩形的性质得出OP=OC,结合勾股定理求出即可;
(3)当四边形PCP′C′能成为正方形时,PP′⊥CC′且OP=OC,则此时点P必在x轴上,利用公式
=c+b2=0 ①,进而得出OP=OC,点C必在y轴的负半轴上,则b=-c②,求出b,c即可.
(2)当b=2时,y=-x2+2bx+c=-x2+4x+c=-(x-2)2+4+c,则顶点P的坐标为(2,4+c),再利用矩形的性质得出OP=OC,结合勾股定理求出即可;
(3)当四边形PCP′C′能成为正方形时,PP′⊥CC′且OP=OC,则此时点P必在x轴上,利用公式
| 4×(-1)×c-(2b)2 |
| 4×(-1) |
解答: 解:(1)当b=c=1时,y=-x2+2x+1=-(x-1)2+2,
解:(1)当b=c=1时,y=-x2+2x+1=-(x-1)2+2,
∴顶点P的坐标为(1,2);
(2)当b=2时,y=-x2+2bx+c=-x2+4x+c=-(x-2)2+4+c,
∴顶点P的坐标为(2,4+c),
当x=0时,y=c,∴点C的坐标为(0,c),
当四边形PC P′C′为矩形时OP=OC,
即22+(4+c)2=c2,
解得:c=-
;
(3)当四边形PCP′C′能成为正方形时,PP′⊥CC′且OP=OC
此时点P必在x轴上,∴
=c+b2=0 ①,
∵OP=OC,点C必在y轴的负半轴上,∴b=-c②,
由①②得,c=0(舍去),c=-1,b=1.
 解:(1)当b=c=1时,y=-x2+2x+1=-(x-1)2+2,
解:(1)当b=c=1时,y=-x2+2x+1=-(x-1)2+2,∴顶点P的坐标为(1,2);
(2)当b=2时,y=-x2+2bx+c=-x2+4x+c=-(x-2)2+4+c,
∴顶点P的坐标为(2,4+c),
当x=0时,y=c,∴点C的坐标为(0,c),
当四边形PC P′C′为矩形时OP=OC,
即22+(4+c)2=c2,
解得:c=-
| 5 |
| 2 |
(3)当四边形PCP′C′能成为正方形时,PP′⊥CC′且OP=OC
此时点P必在x轴上,∴
| 4×(-1)×c-(2b)2 |
| 4×(-1) |
∵OP=OC,点C必在y轴的负半轴上,∴b=-c②,
由①②得,c=0(舍去),c=-1,b=1.
点评:此题主要考查了矩形的性质以及正方形的性质和二次函数综合等知识,结合正方形的性质得出点P必在x轴上,点C必在y轴的负半轴上是解题关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
下列各式中,为最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0),B(-2,0),C(0,-2),直线x=m(m<-2)与x轴交于点D.
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0),B(-2,0),C(0,-2),直线x=m(m<-2)与x轴交于点D.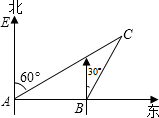 某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁. 如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.
如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.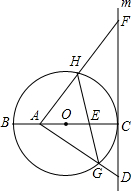 如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.
如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.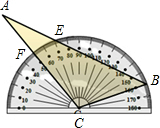 将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为
将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为