题目内容
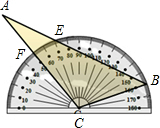将量角器按如图所示的方式放置在三角形纸片上，使点C在半圆圆心上，点B在半圆上，边AB、AC分别交圆于点E、F，点B、E、F对应的读数分别为160°、70°、50°，则∠A的度数为考点：圆周角定理
专题：
分析：连接CE．可得∠ECB=90°，∠ACB=110°，再根据等腰三角形的性质和三角形内角和定理即可求解．
解答：
解：连接CD．
可得∠DCB=160°-70°=90°，∠ACB=160°-50°=110°，
∴∠B=（180°-90°）÷2=45°，
∴∠A=180°-∠ACB-∠B=25°．
故答案为25°．
解：连接CD．可得∠DCB=160°-70°=90°，∠ACB=160°-50°=110°，
∴∠B=（180°-90°）÷2=45°，
∴∠A=180°-∠ACB-∠B=25°．
故答案为25°．
点评：本题考查了等腰三角形的性质和三角形内角和定理，得到∠B和∠ACB的度数是解题的关键．
练习册系列答案
相关题目
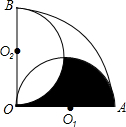如图，扇形OAB的圆心角为90°、半径为2cm，半圆O1和半圆O2的直径分别为OA和OB，则图中阴影部分的面积为已知m，n是方程x2-2
x+1=0的两根，则代数式
的值为（ ）
| 2 |
| m2+n2+3mn |
| A、3 | B、5 | C、9 | D、±3 |
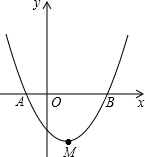如图，二次函数y=