题目内容
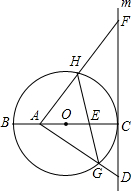 如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.
如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.(1)当A是BO的中点时,求AF的长;
(2)若∠AGH=∠AFD,
①GE与EH相等吗?请说明理由;
②求△AGH的面积.
考点:切线的性质
专题:证明题
分析:(1)由BC=8,A是OB的中点得到AC=6,再根据切线的性质得∠ACD=∠ACF=90°,而∠DAF=90°,根据等角的余角相等得到∠ADC=∠CAF,于是可判△ACD∽△FCA,利用相似比可计算出FC=9,然后在Rt△AFC中,根据勾股定理可计算出AF=3
;
(2)①由于∠AGH=∠AFD,∠DAF=∠HAG=90°,根据等角的余角相等得到∠AHE=∠FAC,则EA=EH,同理可得EA=EG,所以GE=EH
②由于GE=EH,即BC平分GE,根据直径互相平分和垂径定理得到GH是圆O的直径或GH⊥BC,分类讨论:当GH是直径(即A与B重合,E与O重合),则GH=8,
由(1)得到△ACD∽△FCA,利用相似比求出FC=16,则FD=20,再根据相似的性质由△AGH∽△AFD得到
=(
)2,可计算得到S△AGH=
;当GH⊥BC,由于AC垂直平分GH,则AG=AH,且GH∥FD,而∠GAH=90°,所以∠AGH=45°,则∠D=∠AGH=45°,于是可判断△ACD为等腰直角三角形,AC=CD=4,而OC=4,所以A、O点重合,则有AG=AH=4,然后根据三角形面积公式得到△AGH的面积=8.
| 13 |
(2)①由于∠AGH=∠AFD,∠DAF=∠HAG=90°,根据等角的余角相等得到∠AHE=∠FAC,则EA=EH,同理可得EA=EG,所以GE=EH
②由于GE=EH,即BC平分GE,根据直径互相平分和垂径定理得到GH是圆O的直径或GH⊥BC,分类讨论:当GH是直径(即A与B重合,E与O重合),则GH=8,
由(1)得到△ACD∽△FCA,利用相似比求出FC=16,则FD=20,再根据相似的性质由△AGH∽△AFD得到
| S△AGH |
| S△AFD |
| HG |
| FD |
| 64 |
| 5 |
解答:解:(1)∵BC=8,A是OB的中点,
∴AC=6,
又∵DC为⊙O的切线,
∴∠ACD=∠ACF=90°,
∵AD⊥AF,
∴∠DAF=90°,
∴∠ADC=∠CAF,
∴△ACD∽△FCA,
∴CD:AC=AC:FC,即4:6=6:FC,
∴FC=9,
在Rt△AFC中,AF=
=
=3
;
(2)①GE=EH,理由如下:
∵∠AGH=∠AFD,∠DAF=∠HAG=90°,
∴∠AHE=∠FAC,
∴EA=EH,
同理可得EA=EG,
∴GE=EH;
②∵GE=EH,即BC平分GE,
∴GH是圆O的直径或GH⊥BC,
如图1,当GH是直径(即A与B重合,E与O重合),则GH=8,
由(1)得到△ACD∽△FCA,
∴
=
,即
=
,解得FC=16,
∴FD=FC+CD=20,
∵△AGH∽△AFD,
∴
=(
)2,
∴S△AGH=(
)2×
×8×20=
;
如图2,若GH⊥BC,
∴AC垂直平分GH,
∴AG=AH,且GH∥FD,
而∠GAH=90°,则∠AGH=45°,
∴∠D=∠AGH=45°,
∴△ACD为等腰直角三角形,
∴AC=CD=4,
而OC=4,
∴A、O点重合,
∴AG=AH=4,
∴△AGH的面积=
×4×4=8,
即△AGH的面积为8或
.
∴AC=6,
又∵DC为⊙O的切线,
∴∠ACD=∠ACF=90°,
∵AD⊥AF,
∴∠DAF=90°,
∴∠ADC=∠CAF,
∴△ACD∽△FCA,
∴CD:AC=AC:FC,即4:6=6:FC,
∴FC=9,
在Rt△AFC中,AF=
| AC2+CF2 |
| 62+92 |
| 13 |
(2)①GE=EH,理由如下:
∵∠AGH=∠AFD,∠DAF=∠HAG=90°,
∴∠AHE=∠FAC,
∴EA=EH,
同理可得EA=EG,
∴GE=EH;

②∵GE=EH,即BC平分GE,
∴GH是圆O的直径或GH⊥BC,
如图1,当GH是直径(即A与B重合,E与O重合),则GH=8,
由(1)得到△ACD∽△FCA,
∴
| AC |
| FC |
| CD |
| AC |
| 8 |
| FC |
| 4 |
| 8 |
∴FD=FC+CD=20,
∵△AGH∽△AFD,
∴
| S△AGH |
| S△AFD |
| HG |
| FD |
∴S△AGH=(
| 8 |
| 20 |
| 1 |
| 2 |
| 64 |
| 5 |
如图2,若GH⊥BC,
∴AC垂直平分GH,
∴AG=AH,且GH∥FD,
而∠GAH=90°,则∠AGH=45°,
∴∠D=∠AGH=45°,
∴△ACD为等腰直角三角形,
∴AC=CD=4,
而OC=4,
∴A、O点重合,
∴AG=AH=4,
∴△AGH的面积=
| 1 |
| 2 |
即△AGH的面积为8或
| 64 |
| 5 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理、等腰直角三角形的性质.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

 如图,已知,在平面直角坐标系内,点B的坐标为(6,8),过点B分别向x轴和y轴作垂线,垂足分别为C、A,抛物线y=-
如图,已知,在平面直角坐标系内,点B的坐标为(6,8),过点B分别向x轴和y轴作垂线,垂足分别为C、A,抛物线y=- 如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.
如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变. 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AB=7,AD=4,CA=5,动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C→D→A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD交于点E,与折线A-C-B的交点为Q,设点M的运动时间为t.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AB=7,AD=4,CA=5,动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C→D→A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD交于点E,与折线A-C-B的交点为Q,设点M的运动时间为t.