题目内容
17.某足球协会举办了一次足球联赛,其记分规则如下表:| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
分析 由已知设胜x场,平y场,负z场,首先根据比赛总场次12场,得分19分,建立方程组,用x表示y,z最后关键在于分析到题目中隐含的x≥0,y≥0,z≥0且x,y,z为整数从而建立不等式组求到x的值.
解答 解:设A队胜x场,平y场,负z场,
则$\left\{\begin{array}{l}{x+y+z=12}\\{3x+2y=19}\end{array}\right.$,
用x表示y,z解得$\left\{\begin{array}{l}{y=19-3x}\\{z=2x-7}\end{array}\right.$,
∵x≥0,y≥0,z≥0且x,y,z均为整数,
∴$\left\{\begin{array}{l}{x≥0}\\{19-3x≥0}\\{2x-7≥0}\end{array}\right.$,
解之得3$\frac{1}{2}$≤x≤6$\frac{1}{3}$,
∴x=4,5,6
即A队胜,平,负有3种情况,分别是
①A队胜4场平7场负1场;
②A队胜5场平4场负3场;
③A队胜6场平1场负5场.
点评 此题主要考查了三元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组,求出整数解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在△ABC中,∠C=90°,∠A=60°,AC=1,D在BC上,E在AB上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE的长为( )
| A. | $4-2\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\frac{1}{2}(\sqrt{3}-1)$ |
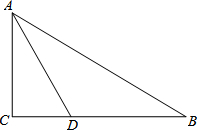 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.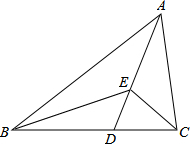 如图,AD是△ABC的角平分线,点E为AD边上一点,且∠BEC=2∠BAC=120°.若BE=2CE,AE=2$\sqrt{3}$,则BC的长为7.
如图,AD是△ABC的角平分线,点E为AD边上一点,且∠BEC=2∠BAC=120°.若BE=2CE,AE=2$\sqrt{3}$,则BC的长为7. 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )



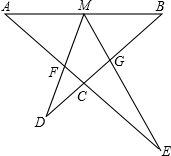 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.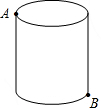 如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?
如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?