题目内容
5.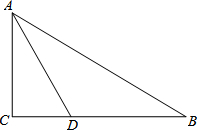 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.(1)动手操作:利用尺规作⊙O,使⊙O经过点A、D,且圆心O在AB上;并标出⊙O与AB的另一个交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①判断直线BC与⊙O的位置关系,并说明理由;
②若AB=6,BD=2$\sqrt{3}$,求线段BD、BE与劣弧$\widehat{DE}$所围成的图形面积(结果保留根号和π).
分析 (1)根据题意得:O点应该是AD垂直平分线与AB的交点;
(2)①由∠BAC的角平分线AD交BC边于D,与圆的性质可证得AC∥OD,又由∠C=90°,则问题得证;
②设⊙O的半径为r.则在Rt△OBD中,利用勾股定理列出关于r的方程,通过解方程即可求得r的值;然后根据扇形面积公式和三角形面积的计算可以求得“线段BD、BE与劣弧DE所围成的图形面积为:S△ODB-S扇形ODE=2$\sqrt{3}$-$\frac{2}{3}$π”.
解答 解:(1)如图1;
(2)①如图1,连接OD,
∵OA=OD,
∴∠OAD=∠ADO,
∵∠BAC的角平分线AD交BC边于D,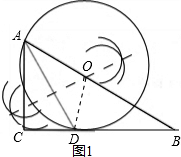
∴∠CAD=∠OAD,
∴∠CAD=∠ADO,
∴AC∥OD,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
即直线BC与⊙O的切线,
∴直线BC与⊙O的位置关系为相切;
(2)如图2,设⊙O的半径为r,则OB=6-r,又BD=2$\sqrt{3}$,
在Rt△OBD中,
OD2+BD2=OB2,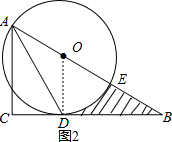
即r2+(2$\sqrt{3}$ )2=(6-r)2,
解得r=2,OB=6-r=4,
∴∠DOB=60°,
∴S扇形ODE=$\frac{60×π{×2}^{2}}{360}$=$\frac{2}{3}$π,
S△ODB=$\frac{1}{2}$OD•BD=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∴线段BD、BE与劣弧DE所围成的图形面积为:S△ODB-S扇形ODE=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 此题主要考查了切线的判定与性质以及扇形面积与三角形面积的求解方法等知识,注意数形结合思想的应用是解答此题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
10.在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为( )
| A. | y=x | B. | y=x-1 | C. | y=x+1 | D. | y=-x+1 |
17.某足球协会举办了一次足球联赛,其记分规则如下表:
当比赛进行到第二轮结束(每队均需比赛12场)时,A队共积19分,问A队胜,平,负各几场?
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |




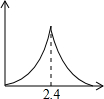
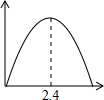
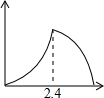
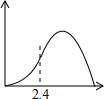
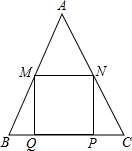 如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )