题目内容
4.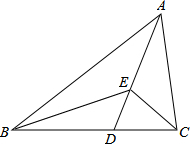 如图,AD是△ABC的角平分线,点E为AD边上一点,且∠BEC=2∠BAC=120°.若BE=2CE,AE=2$\sqrt{3}$,则BC的长为7.
如图,AD是△ABC的角平分线,点E为AD边上一点,且∠BEC=2∠BAC=120°.若BE=2CE,AE=2$\sqrt{3}$,则BC的长为7.
分析 过E作MN⊥AD,交AB、AC分别于点M、N,易证△AMN是等边三角形,证明△BME∽△ENC,根据相似三角形的对应边的比相等即可求得BM、CN的长,作CG⊥AB于点G,在直角△BCG中,利用勾股定理求解.
解答 解:过E作MN⊥AD,交AB、AC分别于点M、N.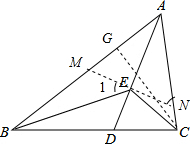
∵AD平分∠BAC,即∠BAD=∠CAD,
∴在△AEM和△AEN中,
$\left\{\begin{array}{l}{∠BAD=∠DAC}\\{AE=AE}\\{∠AEM=∠AEN}\end{array}\right.$,
∴△AEN≌△AEN.
∴AM=AN,
又∵∠BAC=60°,
∴△AMN是等边三角形.
∴ME=EN=AE•tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
∵∠ANE=∠NEC+∠NCE=60°,∠1+∠NEC=180°-∠BEC=60°,
∴∠1=∠NCE,
∴△BME∽△ENC,
∴$\frac{ME}{NC}$=$\frac{BM}{EN}$=$\frac{BE}{EC}$=$\frac{2}{1}$,
∴BM=4,CN=1.
∵AM=AN=4,
∴BM=4,CN=1.
∵AM=AN=4,
∴AB=8,AC=5.
作CG⊥AB于点G.
则CG=$\frac{5\sqrt{3}}{2}$,BG=$\frac{11}{2}$.
∴BC=$\sqrt{C{G}^{2}+B{G}^{2}}$=7.
故答案是:7.
点评 本题考查了相似三角新的判定与性质,以及勾股定理的应用,正确作出辅助线是解决本题的关键.

练习册系列答案
相关题目
12.-3的倒数是( )
| A. | 3 | B. | -3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
10.在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为( )
| A. | y=x | B. | y=x-1 | C. | y=x+1 | D. | y=-x+1 |
17.某足球协会举办了一次足球联赛,其记分规则如下表:
当比赛进行到第二轮结束(每队均需比赛12场)时,A队共积19分,问A队胜,平,负各几场?
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |




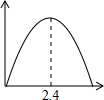
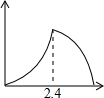
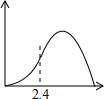
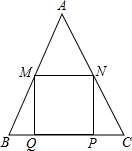 如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
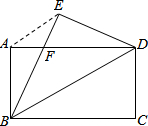 如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.