题目内容
8.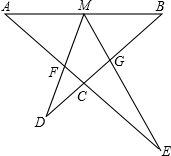 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=4$\sqrt{2}$,AF=3,求FC和FG的长.
分析 (1)根据已知条件,∠DME=∠A=∠B=α,结合图形上的公共角,即可推出△DMG∽△DBM,△EMF∽△EAM,AMF∽△BGM;
(2)根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
解答 解:(1)△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,
∵∠AMD=∠B+∠D,∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=α
∴∠AMF=∠BGM,
∴△AMF∽△BGM,
(2)连接FG,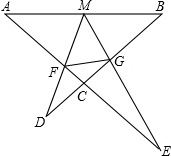
由(1)知,△AMF∽△BGM,
$\frac{BG}{AM}=\frac{BM}{AF}$,BG=$\frac{8}{3}$,∠α=45°,
∴△ABC为等腰直角三角形,
∵M是线段AB中点,
∴AB=4$\sqrt{2}$,AM=BM=2$\sqrt{2}$,
AC=BC=4,CF=AC-AF=1,
CG=4-$\frac{8}{3}=\frac{4}{3}$,
∴由勾股定理得FG=$\frac{5}{3}$.
点评 本题主要考查相似三角形的判定和性质、解直角三角形、等腰三角形的性质,解题的关键找到相似的三角形,根据其性质求出BG、AC的长度.

练习册系列答案
相关题目
17.某足球协会举办了一次足球联赛,其记分规则如下表:
当比赛进行到第二轮结束(每队均需比赛12场)时,A队共积19分,问A队胜,平,负各几场?
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
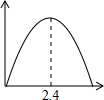
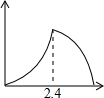
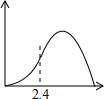
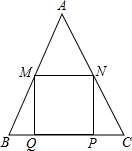 如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )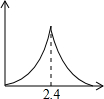
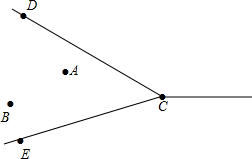 A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:
A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件: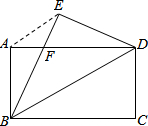 如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE. 如图,已知△ABC.
如图,已知△ABC.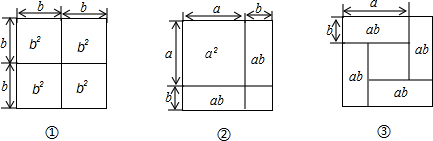
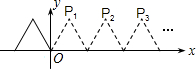 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).