题目内容
3. 在下面的横线上,填上相应的结论:
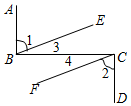
在下面的横线上,填上相应的结论:已知:如图AB⊥BC,BC⊥CD,且∠1=∠2,试说明:AB∥CD,BE∥CF.
理由:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°°(垂直的定义);
∴AB∥CD(垂直于同一条直线的两直线平行);
又∵∠1=∠2(已知),
∴∠EBC=∠BCF,
∴BE∥CF (内错角相等,两直线平行).
分析 由垂直的定义结合已知可得到∠EBC=∠BCF,根据平行线的判定可证得BE∥CF,据此填空即可.
解答 证明:
∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°(垂直的定义),
∴AB∥CD(垂直于同一条直线的两直线平行),
∵∠1=∠2(已知),
∴∠EBC=∠BCF(等式性质),
∴BE∥CF(内错角相等,两直线平行),
故答案为:∠ABC;∠BCD;90;垂直于同一条直线的两直线平行;∠EBC;∠BCF;内错角相等,两直线平行.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
4.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{b}{a}}$ | D. | $\sqrt{4a+4}$ |
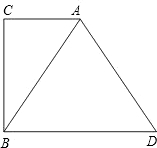 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连结AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连结AD.试判断△ABD的形状,并说明理由. 如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为3$\sqrt{3}$.
如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为3$\sqrt{3}$.