Question

11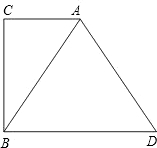．已知：如图，在Rt△ABC中，∠C=90°，过点B作BD∥AC，且BD=2AC，连结AD．试判断△ABD的形状，并说明理由．

Answer 1

分析 在BD上取点E，使BE=AC，连接AE，可证四边形ACBE是平行四边形，又因为∠C=90°，所以四边形ACBE是矩形．因为BD=2AC，则可求得AB=AD，故三角形可判定．

解答 解：△ABD是等腰三角形．
理由如下：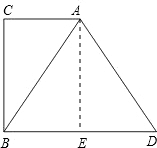
在BD上取点E，使BE=DE，连接AE，
∴BE=$\frac{1}{2}$BD，
∵BD=2AC，
∴BE=AC，
∵BD∥AC，
∴四边形ACBE是平行四边形，
∵∠C=90°，
∴四边形ACBE是矩形，
∴∠AEB=90°，
即AE⊥BD，
∴AB=AD，
∴△ABD是等腰三角形．

点评 本题综合考查了矩形的判定和平行四边形的性质，解本题要充分利用条件，选择适当的方法证明是等腰三角形．