题目内容
13.化简:$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$$÷\frac{x}{x-1}$,并解答:(1)当x=2时,求原式的值;
(2)原式的值能等于-1吗?为什么?
分析 (1)先化简原式,然后将x=2代入原式即可求出答案.
(2)列出方程求出x的值即可.
解答 解:(1)原式=$\frac{(x+1)^{2}}{(x-1)(x+1)}$-$\frac{x(x-1)}{(x-1)^{2}}$×$\frac{x-1}{x}$
=$\frac{x+1}{x-1}$-1
=$\frac{2}{x-1}$,
当x=2时,原式=2;
(2)若原式的值等于-1,即$\frac{2}{x-1}$=-1,解得:x=-1
代入原式检验,分母为0,不合题意,
则原式的值不可能等于-1.
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
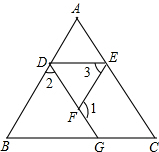 如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由.
如图,已知∠1+∠2=180°,∠B=∠3,判断∠C与∠AED的大小关系,并说明理由. 如图,把直角三角形的直角顶点放在两条平行线a,b上,已知∠1=40°,则∠2=50°.
如图,把直角三角形的直角顶点放在两条平行线a,b上,已知∠1=40°,则∠2=50°.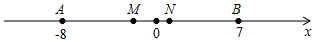
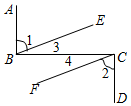 在下面的横线上,填上相应的结论:
在下面的横线上,填上相应的结论: