题目内容
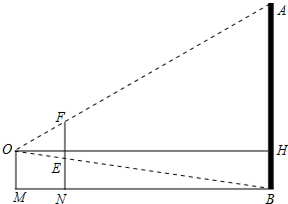一建筑物AB，眼睛位于点O处，用一把长为22cm的刻度尺EF在眼前适当地运动，使眼睛刚好看不见建筑物AB，这时量得眼睛和刻度尺的距离MN为10cm，眼睛距建筑物的距离MB为20m，问建筑物AB多高？考点：相似三角形的应用
专题：计算题
分析：根据题意得到EF=0.22m，MN=0.1m，OH=20m，则OG=MN=0.1m，再证明△OEF∽△OBA，然后利用相似比即可计算出AB的长．
解答：
解：如图，EF=0.22m，MN=0.1m，OH=20m，
所以OG=MN=0.1m，
∵EF∥AB，
∴△OEF∽△OBA，
∴
=
，即
=
，
∴AB=44（m）．
答：建筑物AB的高度为44m．
解：如图，EF=0.22m，MN=0.1m，OH=20m，所以OG=MN=0.1m，
∵EF∥AB，
∴△OEF∽△OBA，
∴
| EF |
| AB |
| OG |
| OH |
| 0.22 |
| AB |
| 0.1 |
| 20 |
∴AB=44（m）．
答：建筑物AB的高度为44m．
点评：本题考查了相似三角形的应用：利用影长测量物体的高度；利用相似测量河的宽度（测量距离）；借助标杆或直尺测量物体的高度．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图，PB切⊙O于B点，直线PO交⊙O于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO交⊙O于点C，连结BC、AF． 
若∠A是锐角，且cosA=
，则（ ）
| 3 |
| 4 |
| A、0°＜∠A＜30° |
| B、30°＜∠A＜45° |
| C、45°＜∠A＜60° |
| D、60°＜∠A＜90° |
如图，圆O的半径为5，BC⊥OA，OD⊥AB，求OD2+CD2的值．
如图，已知△ABC中，AB=AC=10厘米，BC=8厘米，∠A=47°，点D为AB的中点，如果点P在线段BC上以x厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上以y厘米/秒的速度由C点向A点运动．