题目内容
 如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连结BC、AF.
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连结BC、AF. (1)求证:直线PA为⊙O的切线;
(2)若OF:OD=5:4,求S△AOF:S△ABC的比值,
(3)在(2)的条件下,若AF等于3
| 10 |
考点:圆的综合题
专题:综合题
分析:(1)连接OB,根据切线的性质可得∠OBP=90°,根据等腰三角形的性质可得∠AOD=∠BOD,从而可得△OAP≌△OBP,则有∠OAP=∠OBP=90°,即可证到直线PA为⊙O的切线;
(2)易证△ADO∽△ABC,根据相似三角形的性质可得
=
.由OF:OD=5:4可得
=
=
,即可求出
的值;
(3)设OF=5k,则OD=4k,OA=5k,FD=9k,AD=3k,然后在Rt△ADF中运用勾股定理就可解决问题.
(2)易证△ADO∽△ABC,根据相似三角形的性质可得
| S△ADO |
| S△ABC |
| 1 |
| 4 |
| S△AOF |
| S△ADO |
| OF |
| OD |
| 5 |
| 4 |
| S△AOF |
| S△ABC |
(3)设OF=5k,则OD=4k,OA=5k,FD=9k,AD=3k,然后在Rt△ADF中运用勾股定理就可解决问题.
解答:解:(1)连接OB,如图所示,
∵PB切⊙O于B点,
∴∠OBP=90°.
∵OA=OB,OD⊥AB,
∴∠AOD=∠BOD.
在△OAP和△OBP中,
,
∴△OAP≌△OBP(SAS),
∴∠OAP=∠OBP=90°,
∴直线PA为⊙O的切线;
(2)∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠ADO=∠ABC=90°,
∴OD∥BC,
∴△ADO∽△ABC,
∴
=(
)2=
.
∵OF:OD=5:4,
∴
=
=
,
∴
=
•
=
×
=
.
即S△AOF:S△ABC为5:16;
(3)设OF=5k,则OD=4k,OA=5k,FD=9k,
∵∠ADF=90°,
∴AD=3k,
∵AF=3
,
∴AF2=AD2+DF2=90,
∴9k2+81k2=90,
解得k=±1(舍负),
∴OF=5,
即⊙O的半径长为5.
∵PB切⊙O于B点,
∴∠OBP=90°.

∵OA=OB,OD⊥AB,
∴∠AOD=∠BOD.
在△OAP和△OBP中,
|
∴△OAP≌△OBP(SAS),
∴∠OAP=∠OBP=90°,
∴直线PA为⊙O的切线;
(2)∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠ADO=∠ABC=90°,
∴OD∥BC,
∴△ADO∽△ABC,
∴
| S△ADO |
| S△ABC |
| AO |
| AC |
| 1 |
| 4 |
∵OF:OD=5:4,
∴
| S△AOF |
| S△ADO |
| OF |
| OD |
| 5 |
| 4 |
∴
| S△AOF |
| S△ABC |
| S△AOF |
| S△ADO |
| S△ADO |
| S△ABC |
| 5 |
| 4 |
| 1 |
| 4 |
| 5 |
| 16 |
即S△AOF:S△ABC为5:16;
(3)设OF=5k,则OD=4k,OA=5k,FD=9k,
∵∠ADF=90°,
∴AD=3k,
∵AF=3
| 10 |
∴AF2=AD2+DF2=90,
∴9k2+81k2=90,
解得k=±1(舍负),
∴OF=5,
即⊙O的半径长为5.
点评:本题主要考查了圆的切线的判定与性质、相似三角形的判定与性质、勾股定理、三角形的面积等知识,将S△AOF、S△ABC分别与S△ADO相联系是解决第(2)小题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
下列各等式中运用平方差公式计算,错误的是( )
| A、(-a+b)(-a-b)=a2-b2 |
| B、(x+1)(1-x)=1-x2 |
| C、(a+b)2(a-b)2=(a2-b2)2 |
| D、(2x+3)(2x-3)=2x2-9 |
2011年信息产业部的统计数据表明,截止到6月底,我国的电话用户总数达12.1亿,居世界首位,12.1亿用科学记数法表示应为( )
| A、0.120×1010 |
| B、1.21×109 |
| C、12.1×108 |
| D、1.219 |
 如图,在Rt△ABC中,斜边AB=3,若OC∥AB,∠BOC=30°,则下列说法错误的是( )
如图,在Rt△ABC中,斜边AB=3,若OC∥AB,∠BOC=30°,则下列说法错误的是( )A、点A到OB的距离为
| ||||
B、点A到OC的距离为
| ||||
C、点B到OA的距离为
| ||||
D、点B到OC的距离为
|
 如图,直线AD交⊙O于点B,D,⊙O的半径为10cm,AO=16cm,∠A=30°,OC⊥AD于点C,求BC,AB,AD的长.
如图,直线AD交⊙O于点B,D,⊙O的半径为10cm,AO=16cm,∠A=30°,OC⊥AD于点C,求BC,AB,AD的长.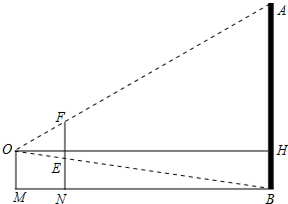 一建筑物AB,眼睛位于点O处,用一把长为22cm的刻度尺EF在眼前适当地运动,使眼睛刚好看不见建筑物AB,这时量得眼睛和刻度尺的距离MN为10cm,眼睛距建筑物的距离MB为20m,问建筑物AB多高?
一建筑物AB,眼睛位于点O处,用一把长为22cm的刻度尺EF在眼前适当地运动,使眼睛刚好看不见建筑物AB,这时量得眼睛和刻度尺的距离MN为10cm,眼睛距建筑物的距离MB为20m,问建筑物AB多高?