题目内容
 如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,∠A=47°,点D为AB的中点,如果点P在线段BC上以x厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上以y厘米/秒的速度由C点向A点运动.
如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,∠A=47°,点D为AB的中点,如果点P在线段BC上以x厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上以y厘米/秒的速度由C点向A点运动.(1)若x=y=3,经过1秒后,此时△BPD与△CQP是否全等?请说明理由.
(2)若x≠y,当x=3,y为何值时,能够使△BPD与△CQP全等?请说明理由.
(3)是否存在点P,使△BPD为等腰三角形?若存在,求此时∠BPD的度数,若不存在,请说明理由.
考点:全等三角形的判定,等腰三角形的判定与性质
专题:动点型
分析:(1)先求得BP=CQ=3,PC=BD=5,然后根据等边对等角求得∠B=∠C,最后根据SAS即可证明;
(2)因为x≠y,所以BP≠CQ,又∠B=∠C,要使△BPD与△CQP全等,只能BP=CP=4,根据全等得出CQ=BD=5,然后根据运动速度求得运动时间,根据时间和CQ的长即可求得Q的运动速度;
(3)有三角形内角和定理和等腰三角形的性质求得∠B的度数.需要分类讨论:∠B=∠BPD和∠B=∠BDP两种情况.
(2)因为x≠y,所以BP≠CQ,又∠B=∠C,要使△BPD与△CQP全等,只能BP=CP=4,根据全等得出CQ=BD=5,然后根据运动速度求得运动时间,根据时间和CQ的长即可求得Q的运动速度;
(3)有三角形内角和定理和等腰三角形的性质求得∠B的度数.需要分类讨论:∠B=∠BPD和∠B=∠BDP两种情况.
解答:解:(1)①∵t=1秒,
∴BP=CQ=3厘米
∵AB=10厘米,D为AB中点,
∴BD=5(厘米)
又∵PC=BC-BP=8-3=5(厘米)
∴PC=BD
∵AB=AC,
∴∠B=∠C,
在△BPD与△CQP中,
,
∴△BPD≌△CQP(SAS);
(2)∵x≠y,
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4,
∵△BPD≌△CPQ,
∴CQ=BD=6.
∴点P的运动时间t=
=
(秒),
此时y=
=
=
(厘米/秒).
(3)存在点P,使△BPD为等腰三角形.理由如下:
∵△ABC中,AB=AC,∠A=47°,
∴∠B=∠C=
=66.5°.
①当∠B=∠BPD=66.5°时,△BPD为等腰三角形
②当∠B=∠BDP=66.5°时,△BPD为等腰三角形,此时∠BPD=180°-2×66.5°=47°.
综上所述,∠BPD的度数是66.5°或47°时,△BPD为等腰三角形.
∴BP=CQ=3厘米
∵AB=10厘米,D为AB中点,
∴BD=5(厘米)
又∵PC=BC-BP=8-3=5(厘米)
∴PC=BD
∵AB=AC,
∴∠B=∠C,
在△BPD与△CQP中,
|
∴△BPD≌△CQP(SAS);
(2)∵x≠y,
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4,

∵△BPD≌△CPQ,
∴CQ=BD=6.
∴点P的运动时间t=
| BP |
| 3 |
| 4 |
| 3 |
此时y=
| CQ |
| t |
| 5 | ||
|
| 15 |
| 4 |
(3)存在点P,使△BPD为等腰三角形.理由如下:
∵△ABC中,AB=AC,∠A=47°,
∴∠B=∠C=
| 180°-47° |
| 2 |
①当∠B=∠BPD=66.5°时,△BPD为等腰三角形
②当∠B=∠BDP=66.5°时,△BPD为等腰三角形,此时∠BPD=180°-2×66.5°=47°.
综上所述,∠BPD的度数是66.5°或47°时,△BPD为等腰三角形.
点评:本题考查了三角形全等的判定和性质,等腰三角形的性质,以及数形结合思想的运用,解题的根据是熟练掌握三角形全等的判定和性质.

练习册系列答案
相关题目
2011年信息产业部的统计数据表明,截止到6月底,我国的电话用户总数达12.1亿,居世界首位,12.1亿用科学记数法表示应为( )
| A、0.120×1010 |
| B、1.21×109 |
| C、12.1×108 |
| D、1.219 |
 如图,在Rt△ABC中,斜边AB=3,若OC∥AB,∠BOC=30°,则下列说法错误的是( )
如图,在Rt△ABC中,斜边AB=3,若OC∥AB,∠BOC=30°,则下列说法错误的是( )A、点A到OB的距离为
| ||||
B、点A到OC的距离为
| ||||
C、点B到OA的距离为
| ||||
D、点B到OC的距离为
|
若方程组
的解x与y的和为3,则a的值为( )
|
| A、7 | B、4 | C、0 | D、-4 |
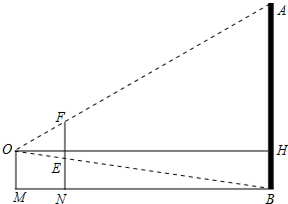 一建筑物AB,眼睛位于点O处,用一把长为22cm的刻度尺EF在眼前适当地运动,使眼睛刚好看不见建筑物AB,这时量得眼睛和刻度尺的距离MN为10cm,眼睛距建筑物的距离MB为20m,问建筑物AB多高?
一建筑物AB,眼睛位于点O处,用一把长为22cm的刻度尺EF在眼前适当地运动,使眼睛刚好看不见建筑物AB,这时量得眼睛和刻度尺的距离MN为10cm,眼睛距建筑物的距离MB为20m,问建筑物AB多高? 如图,A,B,C为⊙O上的三点,且有
如图,A,B,C为⊙O上的三点,且有
 如图,在△ABC中,AD是中线,S△ABD=5cm2,则S△ABC=
如图,在△ABC中,AD是中线,S△ABD=5cm2,则S△ABC=