题目内容
12．
如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，若∠P=46°，则图中度数为46°的角共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 连接BC，OB，由PA、PB是⊙O的切线，可得∠OAP=∠OBP=90°，根据四边形内角和，求出∠AOB，再根据邻补角的定义求得∠BOC=∠P，于是得到结论．
解答 ∵PA、PB是⊙O的切线，A、B为切点，
∴∠OAP=∠OBP=90°．
∴∠AOB+∠P=180°，
∵∠AOB+∠BOC=180°，
∴∠BOC=∠P=46°，
∴图中度数为46°的角只有∠BOC，
故选A．
点评 本题主要考查的是切线的性质，解决本题的关键是连接BC、OB，利用直径对的圆周角是直角，切线的性质，圆周角定理解答．
练习册系列答案
相关题目
2．在实数5，$\frac{22}{7}$，$\sqrt{3}$，$\sqrt{4}$中，无理数是（ ）
| A． | 5 | B． | $\frac{22}{7}$ | C． | $\sqrt{3}$ | D． | $\sqrt{4}$ |
7．以下四个命题：
①有两边和其中一边上的高线对应相等的两个三角形全等；
②有两边和第三边上的高线对应相等的两个三角形全等；
③有两角和其中一角的角平分线对应相等的两个三角形全等；
④有两角和第三个角的角平分线对应相等的两个三角形全等．
其中真命题有（ ）
①有两边和其中一边上的高线对应相等的两个三角形全等；
②有两边和第三边上的高线对应相等的两个三角形全等；
③有两角和其中一角的角平分线对应相等的两个三角形全等；
④有两角和第三个角的角平分线对应相等的两个三角形全等．
其中真命题有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
4．
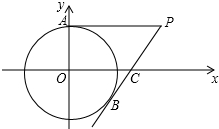如图，在平面直角坐标系中．以点O为圆心，半径为2的圆与y轴交于点A，点P（4，2）是⊙O外一点，连接AP，直线PB与⊙O相切与点B，交PB与⊙O外一点，连接AP，直线PB与⊙O相切于点B，交x轴于点C，则BC的长是（ ）
如图，在平面直角坐标系中．以点O为圆心，半径为2的圆与y轴交于点A，点P（4，2）是⊙O外一点，连接AP，直线PB与⊙O相切与点B，交PB与⊙O外一点，连接AP，直线PB与⊙O相切于点B，交x轴于点C，则BC的长是（ ）| A． | $\frac{5}{4}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{3}{2}$ |
1．
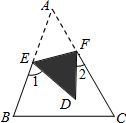如图，△ABC中，∠A=50°，点E、F在AB、AC上，沿EF向内折叠△AEF，得△DEF，则图中∠1+∠2等于（ ）
如图，△ABC中，∠A=50°，点E、F在AB、AC上，沿EF向内折叠△AEF，得△DEF，则图中∠1+∠2等于（ ）| A． | 130° | B． | 120° | C． | 65° | D． | 100° |
2．已知x2+x-1=0，则x3+2x2+3的值是（ ）
| A． | 0 | B． | 3 | C． | 4 | D． | 5 |