题目内容
20.某超市出售茶壶和茶杯,茶壶每只定价24元,茶杯每只定价4元,该超市制定了两种优惠方案:①买一只茶壶送一只茶杯;②按总价的90%付款.某顾客需买茶壶3只,茶杯x(x≥6)只.
(1)若该客户按方案①购买,需付款4x+60元;若该客户按方案②购买,需付款3.6x+64.8元;(都用含x的代数式表示)
(2)当购买茶杯多少只时两种方案价格相同?
分析 (1)根据两种优惠方案分别求得答案即可;
(2)根据两种优惠方案列出不等式解答即可.
解答 解:(1)若该客户按方案①购买,需付款24×3+4(x-3)=4x+60元;
若该客户按方案②购买,需付款(24×3+4x)×90%=3.6x+64.8元;
(2)根据题意可得:4x+60=3.6x+64.8,
解得:x=12.
答:当等于12时,两种方案价格相同.
故答案为:4x+60;3.6x+64.8.
点评 此题考查一元一次方程的应用,找出题目蕴含的数量关系是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
10.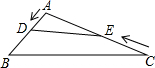 如图,在钝角△ABC中,AB=6cm,AC=12cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是( )
如图,在钝角△ABC中,AB=6cm,AC=12cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是( )
 如图,在钝角△ABC中,AB=6cm,AC=12cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是( )
如图,在钝角△ABC中,AB=6cm,AC=12cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是( )| A. | 3s或4.8s | B. | 3s | C. | 4.5s | D. | 4.5s或4.8s |
15.关于函数y=-2x+1,下列结论正确的是( )
| A. | 图象必经过点(-2,1) | B. | 图象经过第一、二、三象限 | ||
| C. | 当x>$\frac{1}{2}$时,y<0 | D. | y随x的增大而增大 |
5. 如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个小正方形的面积分别为9和25,则正方形A的面积是( )
如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个小正方形的面积分别为9和25,则正方形A的面积是( )
 如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个小正方形的面积分别为9和25,则正方形A的面积是( )
如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个小正方形的面积分别为9和25,则正方形A的面积是( )| A. | 16 | B. | 32 | C. | 34 | D. | 64 |
12. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )
 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
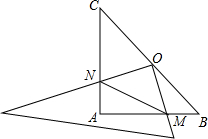 在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,
在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,