题目内容
4.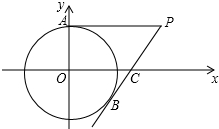 如图,在平面直角坐标系中.以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切与点B,交PB与⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C,则BC的长是( )
如图,在平面直角坐标系中.以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切与点B,交PB与⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C,则BC的长是( )| A. | $\frac{5}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
分析 由AO=2,P的纵坐标为2,得到AP与x轴平行,即PA与AO垂直,即可得到AP为圆O的切线,连接OP,OB,过B作BQ垂直于OC,由切线长定理得到PA=PB=4,PO为角平分线,进而得到一对角相等,根据AP与OC平行,利用两直线平行内错角相等得到一对角相等,等量代换并利用等角对等边得到OC=CP,设OC=x,BC=BP-PC=4-x,OB=2,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可得到结论.
解答 解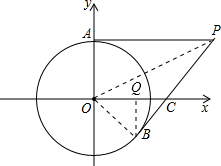 :∵圆O的半径为2,P(4,2),
:∵圆O的半径为2,P(4,2),
∴AP⊥OA,
则AP为圆O的切线,
如图,连接OP,OB,过B作BQ⊥OC,
∵PA、PB为圆O的切线,
∴∠APO=∠BPO,PA=PB=4,
∵AP∥OC,
∴∠APO=∠POC,
∴∠BPO=∠POC,
∴OC=CP,
在Rt△OBC中,设OC=PC=x,则BC=PB-PC=4-x,OB=2,
根据勾股定理得:OC2=OB2+BC2,即x2=4+(4-x)2,
解得:x=2.5,
∴BC=4-x=1.5,
故选:D.
点评 此题考查了切线的性质与判定,坐标与图形性质,勾股定理,平行线的性质,以及切线长定理,熟练掌握切线的性质与判定是解本题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
15.关于函数y=-2x+1,下列结论正确的是( )
| A. | 图象必经过点(-2,1) | B. | 图象经过第一、二、三象限 | ||
| C. | 当x>$\frac{1}{2}$时,y<0 | D. | y随x的增大而增大 |
12. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )
 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则图中度数为46°的角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.若$\frac{b}{a}=\frac{2}{3}$,则$\frac{a-b}{a}$的值是( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
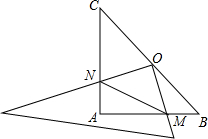 在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,
在你身边45°角的三角板ABC中,AB=AC,∠BAC=90°,O为BC的中点,